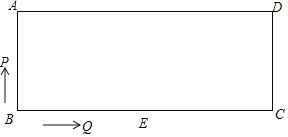Question

【题目】已知：内接于，过点作的切线，交的延长线于点，连接．

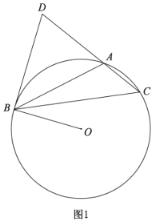
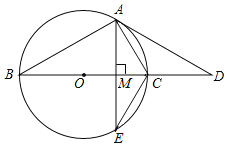
（1）如图1，求证：；

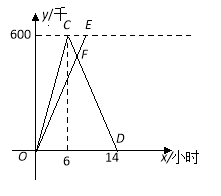
（2）如图2，过点作于点，连接，交于点，，求证：；

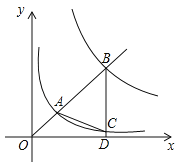
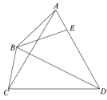
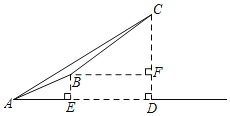
（3）如图3，在（2）的条件下，点为上一点，过点的切线交的延长线于点，连接，交的延长线于点，连接，，点为上一点，连接，若，，，，求的长．

Answer 1

【答案】（1）详见解析；（2）详见解析；（3）

【解析】

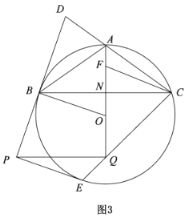
（1）延长BO交于G，连接CG，根据切线的性质可得可证∠DBC＋∠CBG=90°，然后根据直径所对的圆周角是直角可证∠CBG＋∠G=90°，再根据圆的内接四边形的性质可得∠DAB=∠G，从而证出结论；

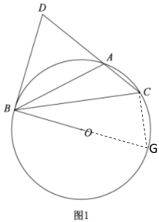
（2）在MB上截取一点H，使AM=MH，连接DH，根据垂直平分线性质可得DH=AD，再根据等边对等角可得∠DHA=∠DAH，然后根据等边对等角和三角形外角的性质证出∠ABC=∠C，可得AB=AC，再根据垂直平分线的判定可得AO垂直平分BC，从而证出结论；

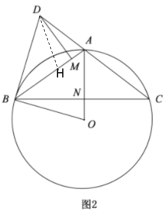
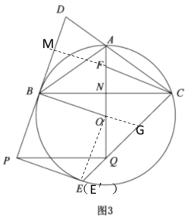
（3）延长CF交BD于M，延长BO交CQ于G，连接OE，证出tan∠BGE=tan∠ECF=2，然后利用AAS证出△CFN≌△BON，可设CF=BO=r，ON=FN=a，则OE=r，根据锐角三角函数和相似三角形即可证出四边形OBPE为正方形，利用r和a表示出各线段，最后根据，即可分别求出a和CF．

解：（1）延长BO交于G，连接CG

∵BD是的切线

∴∠OBD=90°

∴∠DBC＋∠CBG=90°

∵BG为直径

∴∠BCG=90°

∴∠CBG＋∠G=90°

∴∠DBC=∠G

∵四边形ABGC为的内接四边形

∴∠DAB=∠G

∴∠DAB=∠DBC

（2）在MB上截取一点H，使AM=MH，连接DH

∴DM垂直平分AH

∴DH=AD

∴∠DHA=∠DAH

∵，

∴AD=BH

∴DH=BH

∴∠HDB=∠HBD

∴∠DHA=∠HDB＋∠HBD=2∠HBD

由（1）知∠DAB=∠DBC

∴∠DHA=∠DAB=∠DBC

∴∠DBC =2∠HBD

∵∠DBC =∠HBD＋∠ABC

∴∠HBD=∠ABC，∠DBC=2∠ABC

∴∠DAB=2∠ABC

∵∠DAB=∠ABC＋∠C

∴∠ABC=∠C

∴AB=AC

∴点A在BC的垂直平分线上

∵点O也在BC的垂直平分线上

∴AO垂直平分BC

∴

（3）延长CF交BD于M，延长BO交CQ于G，连接OE，

∵

∴∠DMC=90°

∵∠OBD=90°

∴∠DMC=∠OBD

∴CF∥OB

∴∠BGE=∠ECF，∠CFN=∠BON，

∴tan∠BGE=tan∠ECF=2

由（2）知OA垂直平分BC

∴∠CNF=∠BNO=90°，BN=CN

∴△CFN≌△BON

∴CF=BO，ON=FN，设CF=BO=r，ON=FN=a，则OE=r

∵

∴OQ=2a

∵CF∥OB

∴△QGO∽△QCF

∴

即

∴OG=

过点O作OE′⊥BG，交PE于E′

∴OE′=OG·tan∠BGE=r=OE

∴点E′与点E重合

∴∠EOG=90°

∴∠BOE=90°

∵PB和PE是圆O的切线

∴∠OBP=∠OEP=∠BOE=90°，OB=OE=r

∴四边形OBPE为正方形

∴∠BOE=90°，PE=OB=r

∴∠BCE=∠BOE==45°

∴△NQC为等腰直角三角形

∴NC=NQ=3a，

∴BC=2NC=6a

在Rt△CFN中，CF=

∵

∴PQ∥BC

∴∠PQE=∠BCG

∵PE∥BG

∴∠PEQ=∠BGC

∴△PQE∽△BCG

∴

即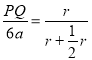

解得：PQ=4a

∵，

∴4a＋2a=

解得：a=

∴CF==10