题目内容
如图,点A是双曲线y=| k |
| x |
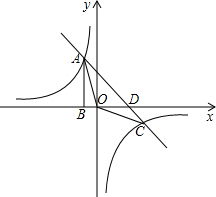 B,且S△ABO=
B,且S△ABO=| 5 |
| 2 |
(1)求这两个函数的解析式;
(2)求△AOC的面积.
分析:(1)欲求这两个函数的解析式,关键求k值.根据反比例函数性质,k绝对值为5且为负数,由此即可求出k;
(2)交点A、C的坐标是方程组
的解,解之即得;从图形上可看出△AOC的面积为两小三角形面积之和,根据三角形的面积公式即可求出.
(2)交点A、C的坐标是方程组
|
解答:解:(1)设A点坐标为(x,y),且x<0,y>0,
则S△ABO=
•|BO|•|BA|=
•(-x)•y=
,
∴xy=-5,
又∵y=
,
即xy=k,
∴k=-5,
∴所求的两个函数的解析式分别为y=-
,y=-x+4;
(2)由y=-x+4,
令y=0,得x=4.
∴直线y=-x+4与x轴的交点D的坐标为(4,0),
A、C两点坐标满足
,解得:
,
∴交点A为(-1,5),C为(5,-1),
∴S△AOC=S△ODA+S△ODC=
•|OD|•(|y1|+|y2|)=
×4×(5+1)=12.
则S△ABO=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∴xy=-5,
又∵y=
| k |
| x |
即xy=k,
∴k=-5,
∴所求的两个函数的解析式分别为y=-
| 5 |
| x |
(2)由y=-x+4,
令y=0,得x=4.
∴直线y=-x+4与x轴的交点D的坐标为(4,0),
A、C两点坐标满足
|
|
|
∴交点A为(-1,5),C为(5,-1),
∴S△AOC=S△ODA+S△ODC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题首先利用待定系数法确定函数解析式,然后利用解方程组来确定图象的交点坐标,及利用坐标求出线段和图形的面积.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 如图,点A是双曲线
如图,点A是双曲线 (2013•萧山区模拟)如图,点P是双曲线
(2013•萧山区模拟)如图,点P是双曲线 如图,点P是双曲线y=
如图,点P是双曲线y= (2013•南通二模)如图,点A是双曲线y=
(2013•南通二模)如图,点A是双曲线y= 如图,点M是双曲线y=
如图,点M是双曲线y=