题目内容
【题目】在综合实践课上,老师以“含30°的三角板和等腰三角形纸片”为模具与同学们开展数学活动.
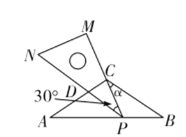
已知,在等腰三角形纸片ABC中,CA=CB=5,∠ACB=120°,将一块含30°角的足够大的直角三角尺PMN(∠M=90°,∠MPN=30°)按如图所示放置,顶点P在线段BA上滑动(点P不与A,B重合),三角尺的直角边PM始终经过点C,并与CB的夹角∠PCB=α,斜边PN交AC于点D.
(1)特例感知
当∠BPC=110°时,α= °,点P从B向A运动时,∠ADP逐渐变 (填“大”或“小”).
(2)合作交流
当AP等于多少时,△APD≌△BCP,请说明理由.
(3)思维拓展
在点P的滑动过程中,△PCD的形状可以是等腰三角形吗?若可以,请求出夹角α的大小;若不可以,请说明理由.
【答案】(1)40°,小;(2)当AP=5时,△APD≌△BCP,理由详见解析;(3)当α=45°或90°时,△PCD是等腰三角形.
【解析】
(1)先根据三角形内角和定理求出∠B的度数,再一次运用三角形内角和定理即可求出![]() 的度数;根据三角形内角和定理即可判断点P从B向A运动时,∠ADP的变化情况;
的度数;根据三角形内角和定理即可判断点P从B向A运动时,∠ADP的变化情况;
(2)先根据三角形外角等于与它不相邻的两个内角和得到∠APC=∠B+α=30°+∠PCB,再证明∠APD=∠BCP,根据全等三角形的判定定理,即可得到当AP=5时,△APD≌△BCP.
(3)根据等腰三角形的判定,分三种情况讨论即可得到;
解:(1)∵CA=CB=5,∠ACB=120°,
∴∠B=∠A=![]() =30°,
=30°,
∴![]() ,
,
∵三角尺的直角边PM始终经过点C,
∴再移动的过程中,∠APN不断变大,∠A的度数没有变化,
∴根据三角形的内角和定理,得到∠ADP逐渐变小;
故答案为:40°,小.
(2)当AP=5时,△APD≌△BCP.
理由如下:∵∠ACB=120°,CA=CB,
∴∠A=∠B=30°.
又∵∠APC是△BPC的一个外角,
∴∠APC=∠B+α=30°+∠PCB,
∵∠APC=∠DPC+∠APD=30°+∠APD,
∴∠APD=∠BCP,
当AP=BC=5时,
在△APD和△BCP中,
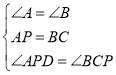
∴△APD≌△BCP(ASA);
(3)△PCD的形状可以是等腰三角形.
根据题意得:∠PCD=120°﹣α,∠CPD=30°,
有以下三种情况:
①当PC=PD时,△PCD是等腰三角形,
∴∠PCD=∠PDC=![]() =75°,即120°﹣α=75°,
=75°,即120°﹣α=75°,
∴α=45°;
②当DP=DC时,△PCD是等腰三角形,
∴∠PCD=∠CPD=30°,即120°﹣α=30°,
∴α=90°;
③当CP=CD时,△PCD是等腰三角形,
∴∠CDP=∠CPD=30°,
∴∠PCD=180°﹣2×30°=120°,
即120°﹣α=120°,
∴α=0°,
此时点P与点B重合,不符合题意,舍去.
综上所述,当α=45°或90°时,△PCD是等腰三角形.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案