题目内容
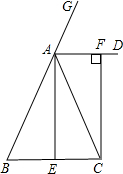
如图，在正方形ABCD中，点E、F分别在CD、BC上，且BF=CE，连结BE、AF相交于点G，则下列结论：①BE=AF；②∠DAF=∠BEC；③∠AFB+∠BEC=90°；④AF⊥BE中正确的有（ ）
| A．①②③ | B．②③④ | C．①②③④ | D．①②④ |
∵四边形ABCD是正方形，
∴∠ABF=∠C=90°，AB=BC，
∵BF=CE，
∴△ABF≌△BCE．
∴AF=BE．（①正确）
∠BAF=∠CBE，∠BFA=∠BEC，（③错误）
∵∠BAF+∠DAF=90°，∠BAF+∠BFA=90°，
∴∠DAF=∠BEC．（②正确）
∵∠BAF=∠CBE，∠BAF+∠AFB=90°，
∴∠CBE+∠AFB=90°，
∴AF⊥BE．（④正确）
所以正确的是①②④．
故选D．
∴∠ABF=∠C=90°，AB=BC，
∵BF=CE，
∴△ABF≌△BCE．
∴AF=BE．（①正确）
∠BAF=∠CBE，∠BFA=∠BEC，（③错误）
∵∠BAF+∠DAF=90°，∠BAF+∠BFA=90°，
∴∠DAF=∠BEC．（②正确）
∵∠BAF=∠CBE，∠BAF+∠AFB=90°，
∴∠CBE+∠AFB=90°，
∴AF⊥BE．（④正确）
所以正确的是①②④．
故选D．
练习册系列答案
学业测评一课一测系列答案
相关题目
