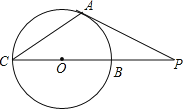
��Ŀ����
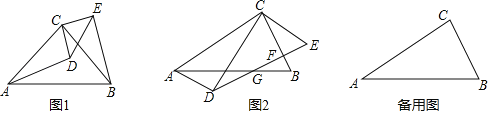
����Ŀ����������ȫ�غϵľ���ֽƬ��������һ���Ƶ�A˳ʱ����ת90����õ�����AMEF����ͼ1��������BD��MF����BD��16cm����ADB��30����
��1����̽���߶�BD ���߶�MF��������ϵ��λ�ù�ϵ����˵�����ɣ�
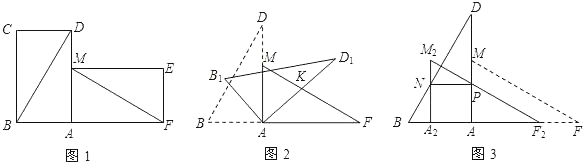
��2������BCD ����MEF ��ȥ������ABD�Ƶ�A˳ʱ����ת����AB1D1����AD1��FM �ڵ�K����ͼ2��������ת��Ϊ����0��������90����������AFK Ϊ����������ʱ�������Ķ�����
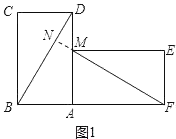
��3��������AFM��AB����ƽ�Ƶõ���A2F2M2����ͼ3����F2M2��AD���ڵ�P��A2M2��BD���ڵ�N����NP��ABʱ����ƽ�Ƶľ��룮
���𰸡���1��BD��MF��BD��MF�����ɼ���������2�����Ķ���Ϊ60����15������3��ƽ�Ƶľ����ǣ�12��4![]() ��cm��
��cm��
��������
��1���ӳ�FM��BD�ڵ�N������ת�����ʵ���BAD�ա�MAF���Ƴ�BD��MF����ADB����AFM�������ɵá�DNM��90����
��2���������������ۣ��ٵ�AK��FKʱ���ڵ�AF��FKʱ��������ת��������⼴�ɣ�
��3��ƽ�Ƶľ�����A2A�ij��ȣ��ھ���PNA2A�У�A2A��PN�����PN�ij��ȼ��ɣ�����DPN�ס�DAB�ó���Ӧ�߶γɱ��������ɵõ�A2A�Ĵ�С��
�⣺��1�����ۣ�BD��MF��BD��MF��
���ɣ���ͼ1���ӳ�FM��BD�ڵ�N��
������ã���BAD�ա�MAF��
��BD��MF����ADB����AFM��
�֡ߡ�DMN����AMF��
���ADB+��DMN����AFM+��AMF��90����
���DNM��90����
��BD��MF��
��2����ͼ2��
�ٵ�AK��FKʱ����KAF����F��30����
���BAB1��180������B1AD1����KAF��180����90����30����60����
������60����
�ڵ�AF��FKʱ����FAK��![]() ��180������F����75����
��180������F����75����
���BAB1��90������FAK��15����
������15����
�������������Ķ���Ϊ60����15����
��3����ͼ3��
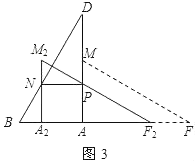
������þ���PNA2A����A2A��x����PN��x��
��Rt��A2M2F2����F2M2��FM��16����A2F2M2����ADB��30����
��A2M2��8��A2F2��8![]() ��
��
��AF2��8![]() ��x��
��x��
�ߡ�PAF2��90������PF2A��30����
��AP��AF2tan30����8��![]() x��
x��
��PD��AD��AP��8![]() ��8+
��8+![]() x��
x��
���DPN�ס�DAB��
��![]() ��
��
��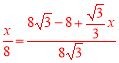 ��
��
���x��12��4![]() ����A2A��12��4
����A2A��12��4![]() ��
��
��ƽ�Ƶľ����ǣ�12��4![]() ��cm��
��cm��