Question

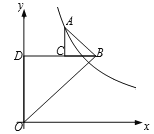
【题目】如图，△ABC和△BOD都是等腰直角三角形，∠ACB＝∠BDO＝90°，且点A在反比例函数（k＞0）的图像上，若OB2－AB2＝10，则k的值为 （ ）

A. 10 B. 5 C. 20 D. 2.5

Answer 1

【答案】B

【解析】分析：设A点坐标为（a，b），根据等腰直角三角形的性质得OB=BD，AB=AC，BC=AC，OD=BD，则OB2-AB2=10，变形为OD2-AC2=5，利用平方差公式得到（OD+AC）（OD-AC）=5，得到ab=5，根据反比例函数图象上点的坐标特征易得k=5．

详解：设A点坐标为（a，b），

∵△ABC和△BOD都是等腰直角三角形，

∴AB=AC，OB=BD，BC=AC，OD=BD

∵OB2-AB2=10，

∴2OD2-2AC2=10，即OD2-AC2=5，

∴（OD+AC）（OD-AC）=5，

∴ab=5，

∴k=5．

故选B．