题目内容
【题目】如图,在![]() 中,
中,![]() 是直径,
是直径,![]() 是弦,
是弦,![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,
,![]() .
.
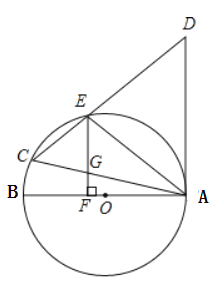
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)过点![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() ,已知
,已知![]() ,
,![]() .求
.求![]() 的长;
的长;
(3)在(2)的条件下,求△![]() 的面积.
的面积.
【答案】(1)证明见解析;(2)5;(3)![]() .
.
【解析】
(1)连接BE,由圆周角定理可得∠AEB=90°,∠B+∠EAB=90°,![]() ,从而得到∠DAE+∠EAB=90°,即AD⊥AB,问题得解;
,从而得到∠DAE+∠EAB=90°,即AD⊥AB,问题得解;
(2)延长EF交⊙O于H,证明△EAG∽△CAE,得出![]() ,求出AE长,求出CG=GE=3,则AC=AG+3,可得出
,求出AE长,求出CG=GE=3,则AC=AG+3,可得出![]() ,解出AG=5;
,解出AG=5;
(3)过点G作GM⊥AE,设ME=x,则AM=![]() ,利用勾股定理列方程求ME的长,从而求MG的长,求出△AEG的面积,然后由等高三角形面积比等于底边之比求△ECG得面积,从而使问题得解.
,利用勾股定理列方程求ME的长,从而求MG的长,求出△AEG的面积,然后由等高三角形面积比等于底边之比求△ECG得面积,从而使问题得解.
解:(1)连接BE
在![]() 中,
中,![]() 是直径,
是直径,
∴∠AEB=90°,∠B+∠EAB=90°,![]()
又∵![]()
∴∠DAE+∠EAB=90°,即AD⊥AB
∴![]() 是
是![]() 的切线;
的切线;

(2)延长EF交⊙O于H,
∵EF⊥AB,AB是直径,
∴![]() ,
,
∴∠EBA=∠AEH,
∵∠EAG=∠CAE,
∴△EAG∽△CAE,
∴![]() ,
,
∵AC=AD,
∴∠D=∠C,
∵∠C=∠DAE,
∴∠D=∠DAE,
∴AE=DE=2![]() ,
,
又∠BFE=∠BAD=90°,
∴AD∥EF,
∴∠D=∠CEF,
∴∠C=∠CEF,
∴CG=GE=3,
∴AC=AG+CG=AG+3,
∴![]() ,
,
∴AG=-8(舍)或AG=5,
即AG的长为5.

(3)过点G作GM⊥AE
由(2)可知,AE=![]() ,AG=5,CG=EG=3
,AG=5,CG=EG=3
设ME=x,则AM=![]()
根据勾股定理可得![]() ,解得
,解得![]()
∴MG=![]()
∴![]()
又∵![]()
∴![]()
∴![]() .
.

练习册系列答案
相关题目