题目内容
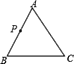
【题目】如图,锐角![]() ,
,![]() 是
是![]() 边上异于
边上异于![]() 、
、![]() 的一点,过点
的一点,过点![]() 作直线截
作直线截![]() ,所截得的三角形与原
,所截得的三角形与原![]() 相似,满足这样条件的直线共有( )条.
相似,满足这样条件的直线共有( )条.
A. 1B. 2C. 3D. 4
【答案】D
【解析】
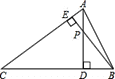
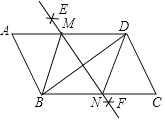
本题可以分两种方法,第一种:利用平行于三角形一边的直线和其他两边相交,所截得的三角形与原三角形相似的判定定理,过点P分别做AC与BC的平行线.第二种:利用两边对应成相等比例且夹角相等的两个三角形相似的判定定理,过P分别做PE交AC或交BC于点E,使使AE:AB=AP:AC或使BP:CB=BE:AB,夹角是公共角∠A或∠B.
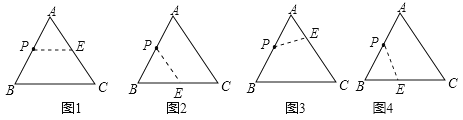
(1)如图1,作PE平行于BC,则△APE![]() △ABC,(2)如图2,作PE平行于AC,则△BPE
△ABC,(2)如图2,作PE平行于AC,则△BPE![]() △BAC,(3)如图3,作PE,使AE:AB=AP:AC,此时∠A.是公共角,△APE
△BAC,(3)如图3,作PE,使AE:AB=AP:AC,此时∠A.是公共角,△APE![]() △ACB,(4)如图4,作PE,使BP:CB=BE:AB.此时∠B是公共角,△PEB
△ACB,(4)如图4,作PE,使BP:CB=BE:AB.此时∠B是公共角,△PEB![]() △ACB
△ACB
所以共有四种画法,即四条直线满足条件,故选D.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
小聪观察上表,得出下面结论:①抛物线与x轴的一个交点为(3,0); ②函数![]() 的最大值为6;③抛物线的对称轴是
的最大值为6;③抛物线的对称轴是![]() ;④在对称轴左侧,y随x增大而增大.其中正确有( )
;④在对称轴左侧,y随x增大而增大.其中正确有( )
A. ①② B. ①③ C. ①②③ D. ①③④