题目内容
【题目】如图，已知函数y=﹣ 
x+b的图象与x轴、y轴分别交于点A、B，与函数y=x的图象交于点M，点M的横坐标为2．
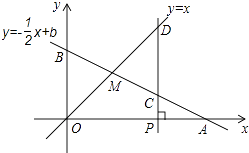
（1）求点A的坐标；
（2）在x轴上有一动点P（a，0）（其中a＞2），过点P作x轴的垂线，分别交函数y=﹣ 
+b和y=x的图象于点C、D．
①若OB=2CD，求a的值；
②是否存在这样的点P，使以B、O、C、D为顶点的四边形是平行四边形？若存在，直接写出点P的坐标；若不存在，请说明理由．
【答案】
（1）解：∵点M的横坐标为2，点M在直线y=x上，
∴M（2，2），
∵点M（2，2）在一次函数y=﹣ 
x+b的图象上，
∴b=3，
∴一次函数的表达式为y=﹣ x+3，
令y=0，得x=6，
∴点A的坐标为（6，0）
（2）解：①由题意得：C（a，﹣12a+3），D（a，a），
∴CD=a﹣（﹣ a+3）= 
a﹣3，
∵OB=2CD．
∴2（ a﹣3）=3，
∴a=3；
②存在，
∵CD∥OB，且以B、O、C、D为顶点的四边形是平行四边形，
∴OB=CD，
∴ a﹣3=3，解得a=4，
∴P（4，0），
即存在满足条件的点P，其坐标为（4，0）．
【解析】（1）可先求得M点坐标，代入直线y=﹣ x+b的解析式，令y=0则可求得A点坐标；（2）①用a可表示出C、D的坐标，从而可表示出CD的长，则由条件可得到关于a的方程，可求得a的值；②当四边形为平行四边形时则可得OB=CD，同①可得到关于a的方程，可求得a的值，则可求得P点坐标．
【考点精析】利用平行四边形的判定对题目进行判断即可得到答案，需要熟知两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形．
