题目内容
【题目】如图,把△ABC放置在每个小正方形边长为1的网格中,点A,B,C均在格点上,建立适当的平面直角坐标系xOy,△ABC与△A′B′C′关于y轴对称.

(1)画出该平面直角坐标系与△A′B′C′.
(2)在y轴上找点P,使PC+PB′的值最小,求点P的坐标与PC+PB'的最小值
【答案】(1)见解析;(2)点P的坐标为(0,﹣1),PC+PB'的最小值为2![]()
【解析】
(1)根据网格即可画出平面直角坐标系和三角形;
(2)根据题意有B′C′与y轴的交点即为点P,再利用勾股定理求出最小值B′C′即可.
解:如图所示:
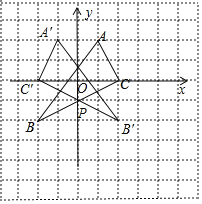
(1)建立平面直角坐标系,
△A′B′C′即为所求作的图形;
(2)B′C′与y轴的交点即为点P,P(0,﹣1)
此时PC+PB′=PC′+PB′=B′C′最小,
B′C′=![]()
答:点P的坐标为(0,﹣1),PC+PB'的最小值为2![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】保险公司车保险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下表:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
该公司随机调查了该险种的300名续保人在一年内的出险情况,得到如下统计图:

(1)样本中,保费高于基本保费的人数为__________名;
(2)已知该险种的基本保费a为6 000元,估计1名续保人本年度的平均保费.





