题目内容
【题目】综合与实践:再探平行四边形的性质
问题情境:
学完平行四边形的有关知识后,同学们开展了再探平行四边形性质的数学活动,以下是“希望小组”得到的一个性质:
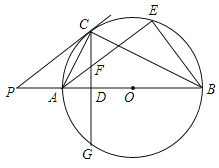
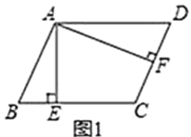
如图1,已知平行四边形![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,
,![]() 垂直
垂直![]() 于点
于点![]() ,则
,则![]() .
.
问题解决:
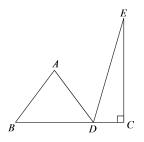
(1)如图2,当![]() 时,
时,![]() 还成立吗?证明你发现的结论;
还成立吗?证明你发现的结论;
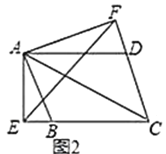
(2)如图2,连接![]() 和
和![]() ,若
,若![]() .求
.求![]() 的度数;
的度数;
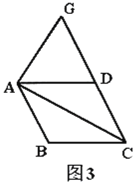
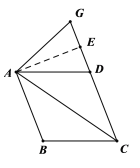
(3)如图3,若![]()
![]() ,
,![]() ,点
,点![]() 是射线
是射线![]() 上一点,且
上一点,且![]() .则
.则![]() _________
_________![]() .(用含
.(用含![]() 的三角函数表示)
的三角函数表示)
【答案】(1)![]() 还成立,证明见解析;(2)
还成立,证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先根据平行四边形的性质、平行线的性质可得![]() ,再根据四边形的内角和可得
,再根据四边形的内角和可得![]() ,然后根据等量代换即可得证;
,然后根据等量代换即可得证;
(2)由(1)可知![]() ,从而可得出
,从而可得出![]() 四点共圆,再根据圆周角定理即可得;
四点共圆,再根据圆周角定理即可得;
(3)如图(见解析),如图,过点A作![]() 于点E,先根据菱形的判定与性质得出
于点E,先根据菱形的判定与性质得出![]() ,
,![]() ,
,![]() ,再根据角的和差、等量代换可得
,再根据角的和差、等量代换可得![]() ,然后根据等腰三角形的判定与性质可得
,然后根据等腰三角形的判定与性质可得![]() ,最后在
,最后在![]() 中,利用余弦三角函数的定义即可得.
中,利用余弦三角函数的定义即可得.
(1)![]() 还成立,证明如下:
还成立,证明如下:
∵四边形![]() 是平行四边形
是平行四边形
∴![]()
∴![]()
在四边形![]() 中,
中,![]() ,
,![]() ,即
,即![]()
∴![]()
∴![]() ;
;
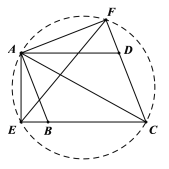
(2)由(1)知,![]()
则如图,![]() 四点共圆
四点共圆
由圆周角定理得:![]() ;
;
(3)如图,过点A作![]() 于点E
于点E
![]() 四边形ABCD是平行四边形,且
四边形ABCD是平行四边形,且![]()
![]() 平行四边形ABCD是菱形
平行四边形ABCD是菱形
![]() ,
,![]() ,
,![]()
![]()
![]()
又![]()
![]()
![]() 是等腰三角形
是等腰三角形
![]() (等腰三角形的三线合一)
(等腰三角形的三线合一)
则在![]() 中,
中,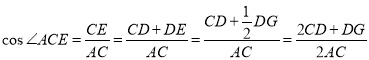
![]()
![]()
![]()
即![]()
故答案为:![]() .
.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
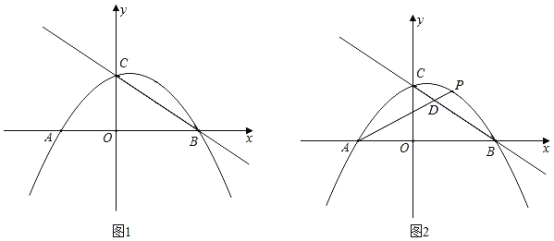
【题目】二次函数![]() (
(![]() ,
,![]() ,
,![]() 是常数,
是常数,![]() )的自变量x与函数值y的部分对应值如下表:
)的自变量x与函数值y的部分对应值如下表:
| … | -1 | 0 | 1 | 3 | … |
| … |
| 3 |
| 3 | … |
且当![]() 时,与其对应的函数值
时,与其对应的函数值![]() .有下列结论:①
.有下列结论:①![]() ;②3是关于
;②3是关于![]() 的方程
的方程![]() 的一个根;③
的一个根;③![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A.0B.1C.2/span>D.3