题目内容
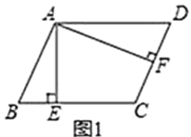
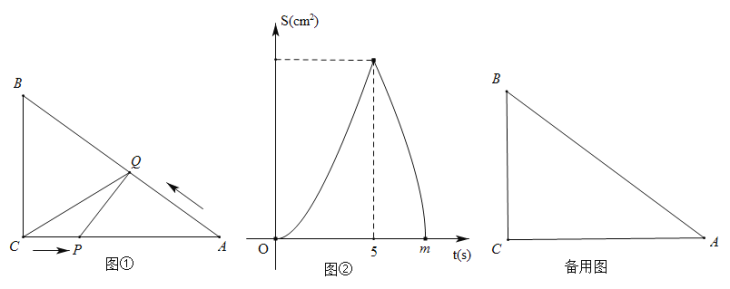
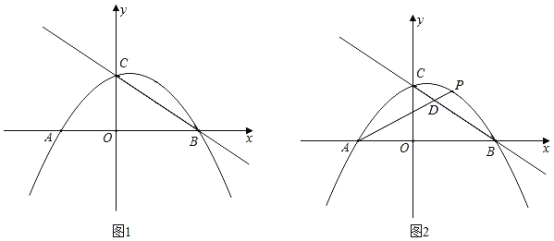
【题目】如图1,二次函数y=ax2+bx+2的图象交x轴于点A(﹣2,0),B(3,0),交y轴于点C,P是第一象限内二次函数图象上的动点.
(1)求这个二次函数的表达式;
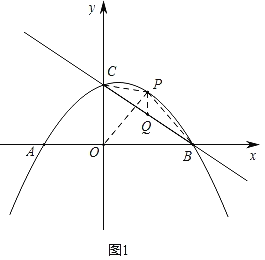
(2)连接PB,PC,PO,若S△POC=S△PBC,求点P的坐标;
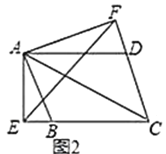
(3)如图2.连接AP,交直线BC于点D,当点D是线段BC的三等分点时,求tan∠ADC的值.
【答案】(1)![]() ;(2)P(1,2);(3)
;(2)P(1,2);(3)![]() .
.
【解析】
(1)将A(﹣2,0),B(3,0)代入函数表达式,即可求解;
(2)S△PBC=S△PQC+S△PQB,S△POC=![]() ,而S△POC=S△PBC,则
,而S△POC=S△PBC,则![]() ,即可求解;
,即可求解;
(3)证明△EAF∽△ADG、△DBG∽△CBO,再分![]() 、
、![]() 两种情况,分别求解即可.
两种情况,分别求解即可.
(1)将A(﹣2,0),B(3,0)代入函数表达式,得![]() ,解得
,解得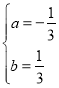 ,
,
∴所求二次函数的表达式为![]() ;
;
(2)过点P作PQ∥y轴交BC于点Q,
将x=0代入![]() 中,得y=2.
中,得y=2.
∴C(0,2).
设直线BC对对应的函数表达式为y=kx+c,
将B(3,0),C(0,2)代入表达式中,
得![]() ,解得
,解得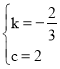 ,
,
∴![]() .
.
设P(x,![]() ),Q(x,
),Q(x,![]() ),
),
∴PQ=yP﹣yQ=![]() ﹣(
﹣(![]() )=
)=![]() .
.
∴S△PBC=S△PQC+S△PQB=![]() =
=![]() =
=![]() ,
,
而S△POC=![]() =
=![]() .
.
∵S△POC=S△PBC,
∴![]() .
.
∴x1=0(舍去),x2=1.
∴P(1,2);
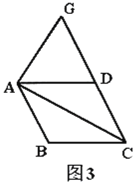
(3)过点A作AE⊥AP交直线BC于点E,过点D作DG⊥x轴于点G,过点E作EF⊥x轴于点F,
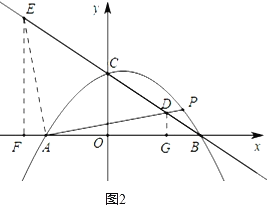
∴∠EFA=∠EAD=∠AGD=90°.
∴∠FEA+∠EAF=90°,∠DAG+∠EAF=90°.
∴∠FEA=∠DAG.
∴△EAF∽△ADG.
∴![]() .
.
∵∠COB=∠DGB=90°,∠CBO=∠CBO,
∴△DBG∽△CBO.
∴![]() .
.
设E(x,![]() ),则AF=﹣2﹣x,EF=
),则AF=﹣2﹣x,EF=![]() .
.
∵点D是线段BC的三等分点,
∴![]() 或
或![]() .
.
当![]() 时,点D(2,
时,点D(2,![]() ).
).
∴AG=4,DG=![]() .
.
∴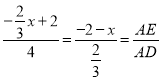 .
.
∴![]() .
.
∴![]() .
.
当![]() 时,点D(1,
时,点D(1,![]() ).
).
∴AG=3,DG=![]() .
.
∴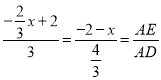 .
.
∴![]() .
.
∴tan∠ADC=![]() =
=![]() .
.