题目内容
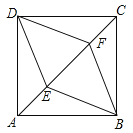
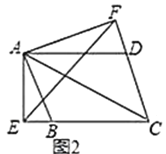
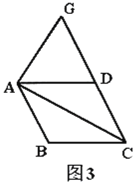
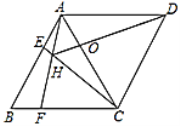
【题目】如图,已知在正方形ABCD中,对角线AC与BD相交于点O,AE,DF分别是∠OAD与∠ODC的平分线,AE的延长线与DF相交于点G,则下列结论:①AG⊥DF;②EF∥AB;③AB=AF;④AB=2EF.其中正确的结论是( )

A.①②B.③④C.①②③D.①②③④
【答案】C
【解析】
①证明∠DAE=∠CDF,进而得∠DAF+∠ADG=90°,便可判断①的正误;
②证明△AGF≌△AGD(ASA),得AG垂直平分DF,得ED=EF,得∠EFD=∠EDF=∠CDF,得EF∥CD,便可判断②的正误;
③由△AGF≌△AGD得AF=AD,便可判断③的正误;
④证明EF=ED=![]() ,由平行于三角形一边的直线所截得的三角形的三边与原三角形的三边对应成比例便可得AB与EF的数量关系,进而判断④的正误.
,由平行于三角形一边的直线所截得的三角形的三边与原三角形的三边对应成比例便可得AB与EF的数量关系,进而判断④的正误.
解:①∵四边形ABCD是正方形,
∴∠CAD=∠BDC=45°,
∵AE,DF分别是∠OAD与∠ODC的平分线,
∴∠DAE=∠CDF,
∵∠ADF+∠CDF=90°,
∴∠DAF+∠ADG=90°,
∴∠AGD=90°,即AG⊥DF,
故①结论正确;
②在△AGF和△AGD中,
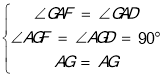 ,
,
∴△AGF≌△AGD(ASA),
∴GF=GD,
∵AG⊥DF,
∴EF=ED,
∴∠EFD=∠EDF=∠CDF,
∴EF∥CD∥AB,
故②正确;
③∵△AGF≌△AGD(ASA),
∴AD=AF=AB,
故③正确;
④∵EF∥CD,
∴∠OEF=∠ODC=45°,
∵∠COD=90°,
∴EF=ED=![]() ,
,
∴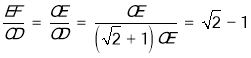 ,
,
∴AB=CD=(![]() +1)EF,
+1)EF,
故④错误.
故选:C.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目