题目内容
【题目】定义:斜率表示一条直线y=kx+b(k≠0)关于橫坐标轴倾斜程度的量,即直线与x轴正方向夹角(倾斜角α)的正切值,表示成k=tanα。
(1)直线y=x-2b的倾斜角α=________。
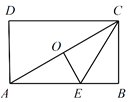
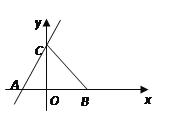
(2)如图,在△ABC中,tanA、tanB是方程x2-(![]() +1)x+
+1)x+![]() =0的两根,且∠A>∠B,B点坐标为(5,0),求出直线AC关系式。
=0的两根,且∠A>∠B,B点坐标为(5,0),求出直线AC关系式。
【答案】(1)45;(2)y=![]() x+5.
x+5.
【解析】(1)根据定义:k=tanα,计算即可;
(2)解方程求出tanA,tanB,解直角三角形即可解决问题;
(1)由题意:tanα=1,∴α=45°.
故答案为:45°.
(2)∵x2﹣(![]() +1)x+
+1)x+![]() =0,
=0,
∴(x﹣![]() )(x﹣1)=0,∴x=
)(x﹣1)=0,∴x=![]() 或1.
或1.
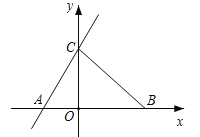
∵∠A>∠B,∴tanA=![]() ,tanB=1.在Rt△BCO中,tanB=
,tanB=1.在Rt△BCO中,tanB=![]() =1.
=1.
∵B(5,0),∴OB=OC=5,∴C(0,5),设直线AC的解析式为y=kx+b,由题意可知:k=![]() ,b=5,∴AC解析式为:y=
,b=5,∴AC解析式为:y=![]() x+5.
x+5.

 阅读快车系列答案
阅读快车系列答案【题目】一手机经销商计划购进华为品牌![]() 型、
型、![]() 型、
型、![]() 型三款手机共
型三款手机共![]() 部,每款手机至少要购进
部,每款手机至少要购进![]() 部,且恰好用完购机款61000元.设购进
部,且恰好用完购机款61000元.设购进![]() 型手机
型手机![]() 部,
部,![]() 型手机
型手机![]() 部.三款手机的进价和预售价如下表:
部.三款手机的进价和预售价如下表:
手机型号 |
|
|
|
进价(单位:元/部) |
|
|
|
预售价(单位:元/部) |
|
|
|
(1)求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)假设所购进手机全部售出,综合考虑各种因素,该手机经销商在购销这批手机过程中需另外支出各种费用共1500元.
①求出预估利润W(元)与x(部)之间的关系式;
(注;预估利润W=预售总额![]() 购机款
购机款![]() 各种费用)
各种费用)
②求出预估利润的最大值,并写出此时购进三款手机各多少部.
【题目】某路公交车从起点经过A、B、C、D站到达终点,一路上下乘客如下表所示。(用正数表示上车的人数,负数表示下车的人数)
| 起点 | A | B | C | D | 终点 |
上车的人数 | 18 | 15 | 12 | 7 | 5 | 0 |
下车的人数 | 0 | -3 | -4 | -10 | -11 |
(1)到终点下车还有_________ 人;
(2)车行驶在那两站之间车上的乘客最多?_______站和________站;
(3)若每人乘坐一站需买票1元,问该车出车一次能收入多少钱?写出算式.