题目内容
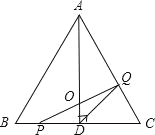
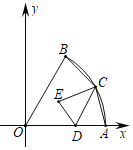
【题目】如图,扇形OAB中,∠AOB=60°,OA=4,点C为弧AB的中点,D为半径OA上一点,点A关于直线CD的对称点为E,若点E落在半径OA上,则OE=______.
【答案】4![]() ﹣4
﹣4
【解析】
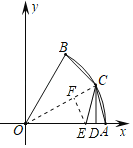
连接OC,作EF⊥OC于F,根据圆心角、弧、弦的关系定理得到∠AOC=30°,根据等腰三角形的性质、三角形内角和定理得到∠ECF=45°,根据正切的定义列式计算,得到答案.
连接OC,作EF⊥OC于F,
∵点A关于直线CD的对称点为E,点E落在半径OA上,
∴CE=CA,
∵![]() =
=![]() ,
,
∴∠AOC=![]() ∠AOB=30°,
∠AOB=30°,
∵OA=OC,
∴∠OAC=∠OCA=75°,
∵CE=CA,
∴∠CAE=∠CEA=75°,
∴∠ACE=30°,
∴∠ECF=∠OCA-∠ACE=75°-30°=45°,
设EF=x,则FC=x,
在Rt△EOF中,tan∠EOF=![]() ,
,
∴OF=![]() =
=![]() ,
,
由题意得,OF+FC=OC,即![]() x+x=4,
x+x=4,
解得,x=2![]() ﹣2,
﹣2,
∵∠EOF=30°,
∴OE=2EF=4![]() ﹣4,
﹣4,
故答案为:4![]() ﹣4.
﹣4.

练习册系列答案
相关题目