题目内容
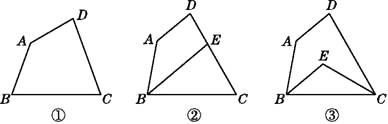
【题目】问题提出:如图1,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP、BP,求AP+![]() BP的最小值.
BP的最小值.
(1)尝试解决:为了解决这个问题,下面给出一种解题思路:如图2,连接CP,在CB上取点D,使CD=1,则有![]() ,又∵∠PCD=∠BCP,∴△PCD∽△BCP.∴
,又∵∠PCD=∠BCP,∴△PCD∽△BCP.∴![]() ,∴PD=
,∴PD=![]() BP,∴AP+
BP,∴AP+![]() BP=AP+PD.
BP=AP+PD.
请你完成余下的思考,并直接写出答案:AP+![]() BP的最小值为 .
BP的最小值为 .
(2)自主探索:在“问题提出”的条件不变的情况下, ![]() AP+BP的最小值为 .
AP+BP的最小值为 .
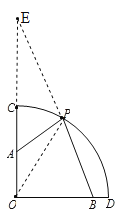
(3)拓展延伸:已知扇形COD中,∠COD=90°,OC=6,OA=3,OB=5,点P是![]() 上一点,求2PA+PB的最小值.
上一点,求2PA+PB的最小值.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)13.
;(3)13.
【解析】试题分析:(1)连结AD,最短为AD=![]() =
=![]() ;
;
(2)连接CP,在CA上取点D,使CD=![]() ,则有
,则有![]() =
=![]() ,可证△PCD∽△ACP,得到PD=
,可证△PCD∽△ACP,得到PD=![]() AP,故
AP,故![]() AP+BP=BP+PD,从而
AP+BP=BP+PD,从而![]() AP+BP的最小值为BD;
AP+BP的最小值为BD;
(3)延长OA到点E,使CE=6,连接PE、OP,可证△OAP∽△OPE,得到EP=2PA,得到2PA+PB=EP+PB,当E、P、B三点共线时,得到最小值.
试题解析:(1)连结AD,最短为AD=![]() =
=![]() ;
;
(2)连接CP,在CA上取点D,使CD=![]() ,则有
,则有![]() =
=![]() ,又∵∠PCD=∠ACP,∴△PCD∽△ACP,∴
,又∵∠PCD=∠ACP,∴△PCD∽△ACP,∴![]() =
=![]() ,∴PD=
,∴PD=![]() AP,∴
AP,∴![]() AP+BP=BP+PD,∴
AP+BP=BP+PD,∴![]() AP+BP的最小值为BD=
AP+BP的最小值为BD=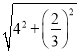 =
=![]() ;
;
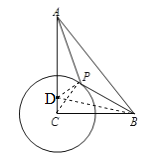
(3)延长OA到点E,使CE=6,连接PE、OP,则OA=3,![]() ,∵∠AOP=∠AOP,∴△OAP∽△OPE,∴
,∵∠AOP=∠AOP,∴△OAP∽△OPE,∴![]() ,∴EP=2PA,∴2PA+PB=EP+PB,当E、P、B三点共线时,取得最小值,为:
,∴EP=2PA,∴2PA+PB=EP+PB,当E、P、B三点共线时,取得最小值,为:![]() =13.
=13.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目