题目内容
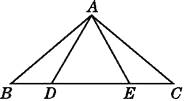
【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,DF⊥AC于点F,下列结论:①∠BAD=∠CAD; ②AD上任意一点到AB,AC的距离相等;
③BD=CD; ④若点P在直线AD上,则PB=PC.其中正确的是( )
A.①
B.①②
C.①②③
D.①②③④
【答案】D
【解析】解:∵AB=AC,
∴△ABC是等腰三角形,
又∵AD⊥BC于D,
∴∠BAD=∠CAD,BD=CD,故①③符合题意;
∵∠BAD=∠CAD,
∴AD上任意一点到AB、AC的距离相等,故②符合题意;
∵AD是BC的中垂线,
∴若点P在直线AD上,则PB=PC,故④符合题意.
故应选:D根据等腰三角形的三线合一得出∠BAD=∠CAD,BD=CD,根据角平分线上的点到角两边的距离相等得出:AD上任意一点到AB、AC的距离相等 ;根据中垂线上的点到线段两边的距离相等得出:若点P在直线AD上,则PB=PC;从而得出答案。

练习册系列答案
相关题目