题目内容
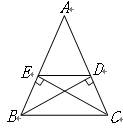
阅读下列材料:如图(1)在四边形ABCD中,若AB=AD,BC=CD,则把这样的四边形称之为“筝形”
解答问题:如图(2)将正方形ABCD绕着点B逆时针旋转一定角度后,得到正方形GBEF,边AD与EF相交于点H.请你判断四边形ABEH是否是“筝形”,说明你的理由.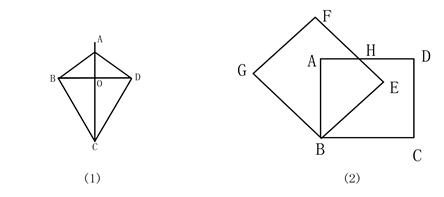
解答问题:如图(2)将正方形ABCD绕着点B逆时针旋转一定角度后,得到正方形GBEF,边AD与EF相交于点H.请你判断四边形ABEH是否是“筝形”,说明你的理由.

是筝形
试题分析:连接BH,根据正方形的性质结合旋转的性质可得∠A=∠E=90°,AB=EB,再结合公共边BH即可证得△HAB≌△HEB,从而证得结论.
连接BH,
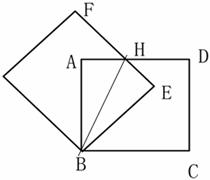
由题意得∠A=∠E=90°,AB=EB,BH=BH
∴△HAB≌△HEB
∴AH=EH,AB=EB
∴四边形ABEH是筝形.
点评:解答本题的关键是读懂题意,准确理解“筝形”的定义,同时熟练掌握正方形的四条边相等,四个角均是直角.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 中,
中,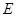 、
、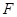 为BC边上两点,且
为BC边上两点,且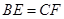 ,
,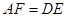 .
.
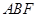 ≌△
≌△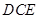 ;
; cm,则宽为( )
cm,则宽为( ) 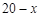

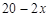
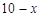
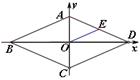
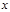 轴上移动.小明同学写出了两个使△POE为等腰三角形的P点坐标(
轴上移动.小明同学写出了两个使△POE为等腰三角形的P点坐标(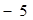 ,
, )和(
)和(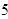 ,
,
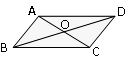
 中,
中,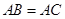 ,
,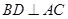 ,
, , 垂足分别为点
, 垂足分别为点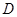 ,
, ,连接
,连接 .试问四边形
.试问四边形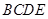 是等腰梯形吗?为什么?
是等腰梯形吗?为什么?