题目内容
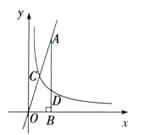
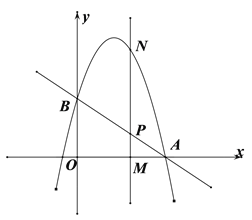
【题目】如图,直线![]() 与x轴交于点
与x轴交于点![]() ,与y轴交于点B,抛物线
,与y轴交于点B,抛物线![]() 经过点
经过点![]() .
.
![]() 求k的值和抛物线的解析式;
求k的值和抛物线的解析式;
![]() 为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点
为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点![]() .
.
![]() 若以O,B,N,P为顶点的四边形OBNP是平行四边形时,求m的值.
若以O,B,N,P为顶点的四边形OBNP是平行四边形时,求m的值.
![]() 当
当![]() 时,求m的值.
时,求m的值.
【答案】⑴![]() ,
, ![]() ⑵
⑵![]() ⑶有两解,N点在AB的上方或下方, m=
⑶有两解,N点在AB的上方或下方, m=![]() 与m=
与m=![]()
【解析】整体分析:
(1)把A(3,0)代入y=kx+2中求k值,把x=0代入y=kx+2,求出B点的坐标,由A,B的坐标求二次函数的解析式;(2)①用含m的式子表示出NP的长,由平行四边形的性质得OB=PN列方程求解;②连接BN,过点B作BN的垂线交x轴于点G,过点G作BA的垂线,垂足为点H, 设GH=BH=t,由![]() ,用t表示AH,AG,由AB=
,用t表示AH,AG,由AB=![]() ,求t的值,求直线BG,BN的解析式,分别与抛物线方程联立求解.
,求t的值,求直线BG,BN的解析式,分别与抛物线方程联立求解.
解:⑴![]() ,
,
二次函数的表达式为![]()
⑵如图,设M(m,0),
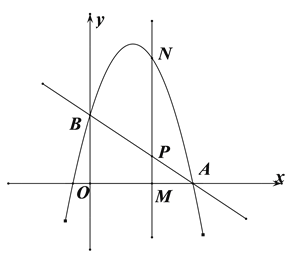
则p(m, ![]() ),N(m,
),N(m, ![]()
![]() =
=![]()
=![]()
由于四边形OBNP为平行四边形得PN=OB=2,
解方程![]() .
.
即![]()
⑶有两解,N点在AB的上方或下方,m=![]() 与m=
与m=![]() .
.
如图连接BN,过点B作BN的垂线交x轴于点G,过点G作BA的垂线,垂足为点H.
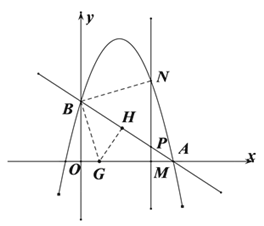
由![]() 得
得![]() ,
,
从而设GH=BH=t,则由![]() ,得AH=
,得AH= ![]() ,
,
由AB=t+ ![]() =
=![]() ,解得t=
,解得t=![]() ,
,
从而OG=OA-AG=3-![]() =
=![]() .即G(
.即G(![]() )
)
由B(0,2),G(![]() )得
)得![]() .
.
将![]() 分别与
分别与![]() 联立,
联立,
解方程组得m=![]() ,m=
,m=![]() .
.
故m=![]() 与m=
与m=![]() .
.

练习册系列答案
相关题目
【题目】甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数![]() 与方差s2如下表所示:
与方差s2如下表所示:
甲 | 乙 | 丙 | 丁 | |
平均数 | 561 | 560 | 561 | 560 |
方差s2 | 3.5 | 3.5 | 15.5 | 16.5 |
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A. 甲B. 乙C. 丙D. 丁