题目内容
【题目】如图，反比例函数
（
， 
）的图象与直线
相交于点C，过直线上点A（1，3）作AB⊥x轴于点B，交反比例函数图象于点D，且AB=3BD.
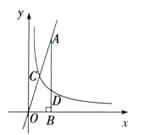
（1）求k的值；
（2）求点C的坐标；
（3）在y轴上确实一点M，使点M到C、D两点距离之和d=MC+MD，求点M的坐标.
【答案】k=1；C（
， 
）；M（（0， 
）
【解析】试题分析：首先根据点A的坐标和AB=3BD求出点B的坐标，从而得出k的值；根据一次函数和反比例函数的解析式得出点C的坐标；作点D关于y轴对称点E，连接CE交y轴于点M，即为所求，设直线CE的解析式为y=kx+b，将点C和点E的坐标代入求出k和b的值，从而得到直线CE的解析式，然后求出直线与y轴的交点坐标，即点M的坐标.
试题解析：（1）∵A（1，3）， ∴OB=1，AB=3， 又AB=3BD， ∴BD=1， ∴B（1，1）， ∴k=1×1=1；
（2）由（1）知反比例函数的解析式为
，
解方程组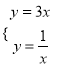
，得
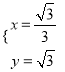或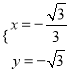
（舍去）， ∴点C的坐标为（
， 
）；
（3）作点D关于y轴对称点E，则E（
,1），连接CE交y轴于点M，即为所求.
设直线CE的解析式为
，则
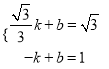，解得
， 
，
∴直线CE的解析式为
， 当x=0时，y=
， ∴点M的坐标为（0， 
）.
练习册系列答案
相关题目
