题目内容
【题目】(8分)如图,△ABC中, ∠BAC=∠ADB,BE平分∠ABC交AD于点E,交AC于点F,过点E作EG//BC交AC于点G.(1)求证: AE=AF; (2)若AG=4,AC=7,求FG的长.

【答案】(1)见解析;(2)1.
【解析】分析:(1)由角平分线的定义和已知条件证出∠AFB=∠AEF,即可得出结论;(2)由SAS证明:△ABF≌△HBF,得出AF=FH,∠AFB=∠HFB,再证明1△AEG≌△FHC,得出AG=FC=4,即可得出结果.
本题解析:
(1)∵BF平分∠ABC
∴∠ABF=∠CBF
∵∠AFB=180°-∠ABF-∠BAF
∠BED=180°-∠CBF-∠ADB
又∵∠BAC=∠ADB
∴∠AFB=∠BED
∵∠AEF=∠BED
∴∠AFB=∠AEF
∴AE=AF
(2)如图,在BC上截取BH=AB,连接FH
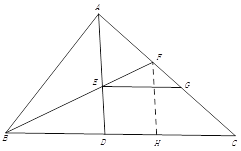
在△ABF和△HBF中
∵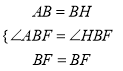
∴△ABF≌△HBF(SAS)
∴AF=FH,∠AFB=∠HFB
∵∠AFB=∠AEF
∴∠HFB=∠AEF
∴AE∥FH
∴∠GAE=∠CFH
∵EG∥BC
∴∠AGE=∠C
∵AE=AF
∴AE=FH
在△AEG和△FHC中
∵
∴△AEG≌△FHC(AAS)
∴AG=FC=4
∴FG=AG+ FC -AC=1

练习册系列答案
相关题目
