题目内容
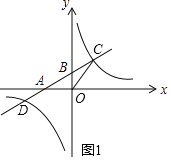
【题目】如图1,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() )两点与x轴,y轴分别交于A、B(0,2)两点,如果
)两点与x轴,y轴分别交于A、B(0,2)两点,如果![]() 的面积为6.
的面积为6.

(1)求点A的坐标;
(2)求一次函数和反比例函数的解析式;
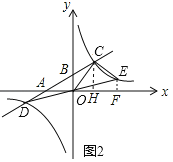
(3)如图2,连接DO并延长交反比例函数的图象于点E,连接CE,求点E的坐标和![]() 的面积
的面积
【答案】(1)A(﹣4,0);(2)![]() ,
,![]() ;(3)
;(3)![]() ,8
,8
【解析】
(1)由三角形面积求出OA=4,即可求得A(-4,0).
(2)利用待定系数法即可求出一次函数的解析式,进而求得C点的坐标,把C点的坐标代入![]() ,求出m的值,得到反比例函数的解析式;
,求出m的值,得到反比例函数的解析式;
(3)先联立两函数解析式得出D点坐标,根据中心对称求得E点的坐标,然后根据三角形的面积公式计算△CED的面积即可.
(1)如图1,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 的面积为6,
的面积为6,
∴![]() ,
,
∵![]() ,
,
∴OA=4,
∴A(﹣4,0);
(2)如图1,把![]() 代入
代入![]() 得
得![]() ,
,
解得![]() ,
,
∴一次函数的解析式为![]() ,
,
把![]() 代入得,
代入得,![]() ,
,
∴![]() ,
,
∵点C在反比例函数![]() 的图象上,
的图象上,
∴m=2×3=6,
∴反比例函数的解析式为![]() ;
;
(3)如图2,作![]() 轴于F,
轴于F,![]() 轴于H,
轴于H,
解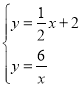 ,得
,得![]() ,
,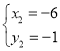 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() =
=![]()

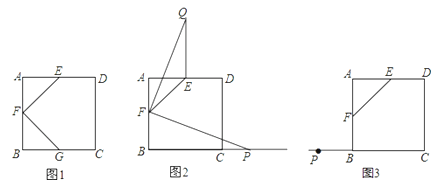
【题目】如图,在平面直角坐标系中,一动点从原点![]() 出发,按向上.向右.向下.向右的方向依次平移,每次移动一个单位,得到
出发,按向上.向右.向下.向右的方向依次平移,每次移动一个单位,得到![]() (0,1),
(0,1),![]() (1,1),
(1,1),![]() (1,0),
(1,0),![]() (2,0),…那么点
(2,0),…那么点![]() 的坐标为__________.
的坐标为__________.

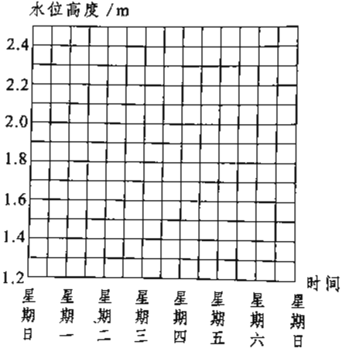
【题目】下表是一个水文站在雨季对某条河一周内水位变化情况的记录.其中,水位上升用正数表示,水位下降用负数表示(水位变化的单位:m).
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
变化 | +0.4 | -0.3 | -0.4 | -0.3 | +0.2 | +0.2 | +0.1 |
注:①表中记录的数据为每天12时的水位与前一天12时的水位的变化量.
②上周日12时的水位高度为2m.
(1)请你通过计算说明本周末水位是上升了还是下降了;
(2)用折线图表示本周每天的水位,并根据折线图说明水位在本周内的升降趋势.