题目内容
【题目】已知:矩形ABCD中,AB=10,AD=8,点E是BC边上一个动点,将△ABE沿AE折叠得到△AB′E。
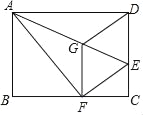
(1)如图(1),点G和点H分别是AD和AB′的中点,若点B′在边DC上。
①求GH的长;
②求证:△AGH≌△B′CE;
(2)如图(2),若点F是AE的中点,连接B′F,B′F∥AD,交DC于I。
①求证:四边形BEB′F是菱形;
②求B′F的长。


【答案】(1)①3;②详见解析;(2)①详见解析;②![]()
【解析】
(1)①由折叠的性质可得出AB=AB′,根据矩形的性质可得出∠ADB′=90°,在Rt△ADB′中,利用勾股定理即可得出B′D的长度,再根据中位线的性质即可得出结论;
②由点G为AD的中点可求出AG的长度,通过边与边的关系可得出B′C=4,由此得出B′C=AG,再通过角的计算得出∠AHG=B′EC,由此即可根据全等三角形的判定定理AAS证出△AGH≌△B′CE;
(2)①连接BF,由平行线的性质结合直角三角的中线的性质即可得知△B′EF为等边三角形,根据折叠的性质即可证出四边形BEB′F是菱形;
②由等边三角形和平行线的性质可得出∠BEF=∠B′EF=60°,再由AB=10利用特殊角的三角函数值即可得出结论.
(1)①∵将△ABE沿AE折叠得到△AB′E
∴AB=AB′
∵四边形ABCD为矩形
∴∠ADB′=90°
在Rt△ADB′中,AD=8,AB′=10
∴B′D=![]() =6
=6
∵点G和点H分别是AD和AB′的中点,∴GH为△ADB′的中位线
∴GH=![]() DB′=3
DB′=3
②证明:∵GH为△ADB′的中位线
∵GH∥DC,AG=![]() AD=4
AD=4
∴∠AHG=∠AB′D
∵∠AB′E=∠ABE=90°
∴∠AB′D+∠CB′E=90°
又∵∠CB′E+∠B′EC=90°
∴∠AHG=B′EC
∵CD=AB=10,DB′=6
∴B′C=4=AG
在△AGH和△B′CE中
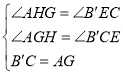
∴△AGH≌△B′CE(AAS).
(2)①证明:
∵将△ABE沿AE折叠得到△AB′E
∴BF=B′F,∠B′EF=∠BEF,BE=B′E
∵B′F∥AD,AD∥BC
∴B′F∥BC
∴∠B′FE=∠BEF=∠B′EF
∵∠AB′E=∠ABE=90°,点F为线段AE的中点
∴B′F=![]() AE=FE
AE=FE
∴△B′EF为等边三角形
∴B′F=B′E
∵BF=B′F,BE=B′E
∴B′F=BF=BE=B′E
∴四边形BEB′F是菱形
②∵△B′EF为等边三角形
∴∠BEF=∠B′EF=60°
∴BE=ABcot∠BEF=10×![]() =
=![]()
∵四边形BEB′F是菱形
∴B′F=BE=![]() .
.