题目内容
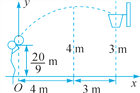
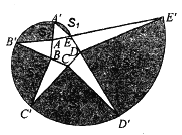
【题目】如图1,在平面直角坐标系中,AB=OB=8,∠ABO=90°,∠yOC=45°,射线OC以每秒2个单位长度的速度向右平行移动,当射线OC经过点B时停止运动,设平行移动x秒后,射线OC扫过Rt△ABO的面积为y.
(1)求y与x之间的函数关系式;
(2)当x=3秒时,射线OC平行移动到O′C′,与OA相交于G,如图2,求经过G,O,B三点的抛物线的解析式;
(3)现有一动点P在(2)中的抛物线上,试问点P在运动过程中,是否存在△POB的面积S=8的情况?若存在,求出点P的坐标,若不存在,请说明理由.
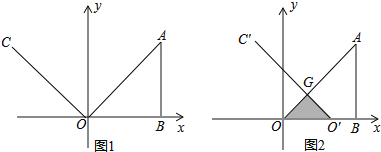
【答案】(1)y=x2;(2)y=﹣![]() x2+
x2+![]() x;(3)点P的坐标为(4﹣
x;(3)点P的坐标为(4﹣![]() ,2)或(4+
,2)或(4+![]() ,2)或(4﹣
,2)或(4﹣![]() ,﹣2)或(4+
,﹣2)或(4+![]() ,﹣2)时,△POB的面积S=8.
,﹣2)时,△POB的面积S=8.
【解析】
(1)判断出△ABO是等腰直角三角形,根据等腰直角三角形的性质可得∠AOB=45°,然后求出AO⊥CO,再根据平移的性质可得AO⊥C′O′,从而判断出△OO′G是等腰直角三角形,然后根据等腰直角三角形的性质列式整理即可得解;
(2)求出OO′,再根据等腰直角三角形的性质求出点G的坐标,然后设抛物线解析式为y=ax2+bx,再把点B、G的坐标代入,利用待定系数法求二次函数解析式解答;
(3)设点P到x轴的距离为h,利用三角形的面积公式求出h,再分点P在x轴上方和下方两种情况,利用抛物线解析式求解即可.
(1)∵AB=OB,∠ABO=90°,
∴△ABO是等腰直角三角形,
∴∠AOB=45°,
∵∠yOC=45°,
∴∠AOC=(90°﹣45°)+45°=90°,
∴AO⊥CO,
∵C′O′是CO平移得到,
∴AO⊥C′O′,
∴△OO′G是等腰直角三角形,
∵射线OC的速度是每秒2个单位长度,
∴OO′=2x,
∴其以OO′为底边的高为x,
∴y=![]() ×(2x)x=x2;
×(2x)x=x2;
(2)当x=3秒时,OO′=2×3=6,
∵![]() ×6=3,
×6=3,
∴点G的坐标为(3,3),
设抛物线解析式为y=ax2+bx,
则![]() ,
,
解得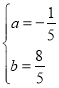 ,
,
∴抛物线的解析式为y=![]() ;
;
(3)设点P到x轴的距离为h,
则S△POB=![]() ×8h=8,
×8h=8,
解得h=2,
当点P在x轴上方时,![]() =2,
=2,
整理得,x2
解得x1=4﹣![]() ,x2=4+
,x2=4+![]() ,
,
此时,点P的坐标为(4﹣![]() ,2)或(4+
,2)或(4+![]() ,2);
,2);
当点P在x轴下方时,![]() =﹣2,
=﹣2,
整理得,x2﹣8x﹣10=0,
解得x1=4﹣![]() ,x2=4+
,x2=4+![]() ,
,
此时,点P的坐标为(4﹣![]() ,﹣2)或(4+
,﹣2)或(4+![]() ,﹣2),
,﹣2),
综上所述,点P的坐标为(4﹣![]() ,2)或(4+
,2)或(4+![]() ,2)或(4﹣
,2)或(4﹣![]() ,﹣2)或(4+
,﹣2)或(4+![]() ,﹣2)时,△POB的面积S=8.
,﹣2)时,△POB的面积S=8.

 孟建平小学滚动测试系列答案
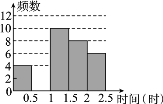
孟建平小学滚动测试系列答案【题目】某中学对本校初中学生完成家庭作业的时间做了总量控制,规定学生每天完成家庭作业的时间少于1.5小时.该校数学课外兴趣小组对本校初中学生回家完成作业的时间作了一次随机抽样调查,并绘制出频数分布表和频数分布直方图的一部分.
时间(时) | 频数 | 频率 |
0≤t<0.5 | 4 | 0.1 |
0.5≤t<1 | a | 0.3 |
1≤t<1.5 | 10 | 0.25 |
1.5≤t<2 | 8 | b |
2≤t<2.5 | 6 | 0.15 |
合计 | 1 |
(1)在频数分布表中,a=________,b=________;
(2)补全频数分布直方图;
(3)请估计该校1400名初中学生中,有多少名学生在1.5小时以内(不包括1.5小时)完成了家庭作业?![]()