题目内容
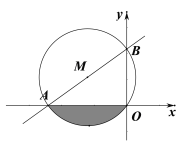
【题目】如图,直线y=![]() x+2与x轴交于点A,与y轴交于点B,抛物线y=﹣
x+2与x轴交于点A,与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过A、B两点,与x轴的另一个交点为 C.
x2+bx+c经过A、B两点,与x轴的另一个交点为 C.
(1)求抛物线的解析式;
(2)根据图象,直接写出满足![]() x+2≥﹣
x+2≥﹣![]() x2+bx+c的x的取值范围;
x2+bx+c的x的取值范围;
(3)设点D为该抛物线上的一点、连结AD,若∠DAC=∠CBO,求点D的坐标.

【答案】(1)![]() ;(2)当x≥0或x≤﹣4;(3)D 点坐标为(0,2)或(2,﹣3).
;(2)当x≥0或x≤﹣4;(3)D 点坐标为(0,2)或(2,﹣3).
【解析】
(1)由直线y=![]() x+2求得A、B的坐标,然后根据待定系数法即可求得抛物线的解析式;
x+2求得A、B的坐标,然后根据待定系数法即可求得抛物线的解析式;
(2)观察图象,找出直线在抛物线上方的x的取值范围;
(3)如图,过D点作x轴的垂线,交x轴于点E,先求出CO=1,AO=4,再由∠DAC=∠CBO,得出tan∠DAC=tan∠CBO,从而有,![]() ,最后分类讨论确定点D的坐标.
,最后分类讨论确定点D的坐标.
解:(1)由y=![]() x+2可得:
x+2可得:
当x=0时,y=2;当y=0时,x=﹣4,
∴A(﹣4,0),B(0,2),
把A、B的坐标代入y=﹣![]() x2+bx+c得:
x2+bx+c得: 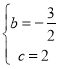 ,,
,,
∴抛物线的解析式为:![]()
(2)当x≥0或x≤﹣4时,![]() x+2≥﹣
x+2≥﹣![]() x2+bx+c
x2+bx+c
(3)如图,过D点作x轴的垂线,交x轴于点E,
由![]() 令y=0,
令y=0,
解得:x1=1,x2=﹣4,
∴CO=1,AO=4,
设点D的坐标为(m,![]() ),
),
∵∠DAC=∠CBO,
∴tan∠DAC=tan∠CBO,
∴在Rt△ADE和Rt△BOC中有![]() ,
,
当D在x轴上方时,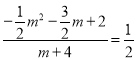
解得:m1=0,m2=﹣4(不合题意,舍去),
∴点D的坐标为(0,2).
当D在x轴下方时,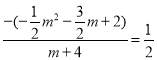
解得:m1=2,m2=﹣4(不合题意,舍去),
∴点D的坐标为(2,﹣3),
故满足条件的D 点坐标为(0,2)或(2,﹣3).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目