Question

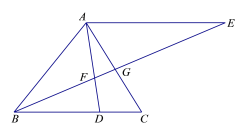
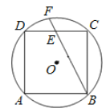
【题目】如图，正方形ABCD内接于⊙O，点E为DC的中点，BE的延长线交⊙O于点F，若⊙O的半径为，则BF的长为________．

Answer 1

【答案】

【解析】

根据正方形的性质以及圆周角定理可得出正方形边长，再利用勾股定理以及三角形面积关系得出即可．

解：如图，连接BD，DF，过点C作CN⊥BF于点N，

∵正方形ABCD内接于⊙O，⊙O的半径为，

∴BD＝2，

∴AD＝AB＝BC＝CD＝2，

∵E为DC的中点，

∴CE＝1．

∴BE＝＝＝．

∵CN·BE＝EC·BC，即CN·＝2，

∴CN＝．

∴EN＝＝＝．

∵BD为⊙O的直径，

∴∠BFD＝90°，

在△CEN和△DEF中，

,

∴△CEN≌△DEF(AAS)．

∴EF＝EN＝．

∴BF＝BE＋EF＝＋＝．

故答案为：.