ƒøƒ⁄»ð
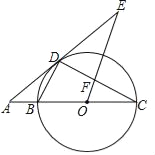
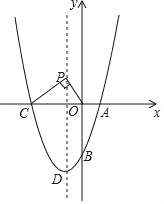
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨∂˛¥Œ∫Ø ˝y=x2+bx+cµƒÕºœÛ”Îx÷·Ωª”⁄A°¢C¡Ωµ„£¨µ„A‘⁄µ„Cµƒ”“±þ£¨”Îy÷·Ωª”⁄µ„B£¨µ„Bµƒ◊¯±ÍŒ™£®0£¨©Å3£©£¨«“OB=OC£¨µ„DŒ™∏√∂˛¥Œ∫Ø ˝ÕºœÛµƒ∂•µ„£Æ
£®1£©«Û’‚∏ˆ∂˛¥Œ∫Ø ˝µƒΩ‚Œˆ Ωº∞∂•µ„Dµƒ◊¯±Í£ª
£®2£©»ÁÕº£¨»Ùµ„PŒ™∏√∂˛¥Œ∫Ø ˝µƒ∂‘≥∆÷·…œµƒ“ªµ„£¨¡¨Ω”PC°¢PO£¨ πµ√°œCPO=90°„£¨«Î«Û≥ˆÀ˘”–∑˚∫œÃ‚“‚µƒµ„Pµƒ◊¯±Í£ª
£®3£©‘⁄∂‘≥∆÷·…œ «∑ҥʑ⁄“ªµ„P£¨ πµ√°œOPCŒ™∂€Ω«£¨»Ù¥Ê‘⁄£¨«Î÷±Ω”–¥≥ˆµ„Pµƒ◊ð◊¯±ÍŒ™ypµƒ»°÷µ∑∂Œß£¨»Ù√ª”–£¨«ÎÀµ√˜¿Ì”…£Æ
°æ¥∞∏°ø£®1£©∂˛¥Œ∫Ø ˝µƒΩ‚Œˆ ΩŒ™y=x2+2x©Å3£¨D£®©Å1£¨©Å4£©£ª£®2£©P£®©Å1£¨![]() £©ªÚ£®©Å1£¨©Å
£©ªÚ£®©Å1£¨©Å![]() £©£ª£®3£©µ±©Å
£©£ª£®3£©µ±©Å![]() £ºyP£º
£ºyP£º![]() «“yP°Ÿ0 ±£¨°œOPC «∂€Ω«£Æ
«“yP°Ÿ0 ±£¨°œOPC «∂€Ω«£Æ
°æΩ‚Œˆ°ø
£®1£©œ»«Û≥ˆµ„C◊¯±Í£¨◊Ó∫Û”√¥˝∂®œµ ˝∑®º¥ø…µ√≥ˆΩ·¬€£ª
£®2£©œ»¿˚”√Õ¨Ω«µƒ”ýΩ«œýµ»£¨≈–∂œ≥ˆ°œCOP=°œCPQ£¨Ω¯∂¯«Û≥ˆPQ£¨º¥ø…µ√≥ˆΩ·¬€£ª
£®3£©ΩË÷˙£®2£©µƒΩ·¬€∫ÕÕº–Œ£¨º¥ø…µ√≥ˆΩ·¬€£Æ
£®1£©°þB£®0£¨©Å3£©£¨°ýOB=3£Æ
°þOB=OC£¨°ýOC=3£¨°ýC£®0£¨©Å3£©£¨°ý![]() £¨°ý
£¨°ý![]() £¨°ý∂˛¥Œ∫Ø ˝µƒΩ‚Œˆ ΩŒ™y=x2+2x©Å3=©Å£®x©Å1£©2©Å4£¨°ýD£®©Å1£¨©Å4£©£ª
£¨°ý∂˛¥Œ∫Ø ˝µƒΩ‚Œˆ ΩŒ™y=x2+2x©Å3=©Å£®x©Å1£©2©Å4£¨°ýD£®©Å1£¨©Å4£©£ª
£®2£©»ÁÕº£¨π˝µ„P◊˜PQ°Õx÷·”⁄µ„Q£¨…ËP£®©Å1£¨p£©£Æ
°þ°œCOP+°œOPQ=90°„£¨°œCPQ+°œOPQ=90°„£¨°ý°œCOP=°œCPQ£¨°ýtan°œCOP=tan°œCPQ£Æ‘⁄Rt°˜QOP÷–£¨tan°œCOP=![]() £Æ‘⁄Rt°˜CPQ÷–£¨tan°œCPQ=
£Æ‘⁄Rt°˜CPQ÷–£¨tan°œCPQ=![]() £¨°ý
£¨°ý![]() £¨°ýPQ2=CQ°¡OQ=2£®¥À¥¶ø…“‘”√…‰”∞∂®¿Ì£¨“≤ø…“‘≈–∂œ≥ˆ°˜CPQ°◊°˜POQ£©£Æ
£¨°ýPQ2=CQ°¡OQ=2£®¥À¥¶ø…“‘”√…‰”∞∂®¿Ì£¨“≤ø…“‘≈–∂œ≥ˆ°˜CPQ°◊°˜POQ£©£Æ
°þPQ£æ0£¨°ýPQ=![]() £¨°ýp=
£¨°ýp=![]() ªÚp=©Å
ªÚp=©Å![]() £¨°ýP£®©Å1£¨
£¨°ýP£®©Å1£¨![]() £©ªÚ£®©Å1£¨©Å
£©ªÚ£®©Å1£¨©Å![]() £©£ª
£©£ª
£®3£©¥Ê‘⁄’‚—˘µƒµ„P£¨¿Ì”…£∫»ÁÕº£¨”…£®2£©÷™£¨yP=![]() ±£¨°œOPC=90°„£Æ
±£¨°œOPC=90°„£Æ
°þyP=0 ±£¨°œOPC «∆ΩΩ«£¨°ýµ±©Å![]() £ºyP£º
£ºyP£º![]() «“yP°Ÿ0 ±£¨°œOPC «∂€Ω«£Æ
«“yP°Ÿ0 ±£¨°œOPC «∂€Ω«£Æ

°æƒø°øƒ≥π´Àæ µ––ƒÍπ§◊ ÷∆£¨÷∞𧵃ƒÍπ§◊ ”…ª˘¥°π§◊ °¢◊°∑ø≤πÃ˘∫Õ“Ω¡∆∑—»˝œÓ◊È≥…£¨æþÃÂπÊ∂®»Áœ¬£∫
œÓƒø | µ⁄“ªƒÍµƒπ§◊ £®ÕÚ‘™£© | “ªƒÍ∫Ûµƒº∆À„∑Ω∑® |
ª˘¥°π§◊ | 1 | √øƒÍµƒ‘ˆ≥§¬ œýÕ¨ |
◊°∑ø≤πÃ˘ | 0.04 | √øƒÍ‘ˆº”0.04 |
“Ω¡∆∑— | 0.1384 | πÃ∂®≤ª±‰ |
£®1£©…˪˘¥°π§◊ √øƒÍ‘ˆ≥§¬ Œ™x£¨”√∫¨xµƒ¥˙ ˝ Ω±Ì æµ⁄»˝ƒÍµƒª˘¥°π§◊ Œ™ ÕÚ‘™£ª
£®2£©ƒ≥»À‘⁄π´Àæπ§◊˜¡À3ƒÍ£¨À˚À„¡À“ªœ¬’‚3ƒÍƒ√µΩµƒ◊°∑ø≤πÃ˘∫Õ“Ω¡∆∑—’˝∫√ «’‚3ƒÍª˘¥°π§◊ ◊Ð∂Óµƒ18 %£¨Œ ª˘¥°π§◊ √øƒÍµƒ‘ˆ≥§¬ «∂ý…Ÿ£ø