题目内容
【题目】如图,在平面直角坐标系中,已知点A(﹣1, ![]() ),B(2,0)在抛物线11:y=ax2+bx+1(a,b为常数,且a≠0)上,直线12经过抛物线11的顶点且与y轴垂直,垂足为点D.
),B(2,0)在抛物线11:y=ax2+bx+1(a,b为常数,且a≠0)上,直线12经过抛物线11的顶点且与y轴垂直,垂足为点D.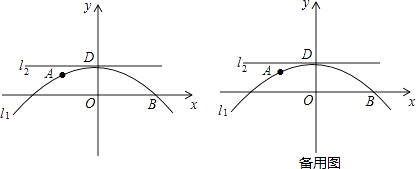
(1)求l1的解析式,并写出它的对称轴和顶点坐标;
(2)设l1上有一动点P从点A出发,沿抛物线从左向右运动,点P的纵坐标yp也随之以每秒2个单位长的速度变化,设点P运动的时间为t(秒),连接OP,以线段OP为直径作⊙F.
①求yp关于t的表达式,并写出t的取值范围;
②当点P在起点A处时,直线l2与⊙F的位置关系是 , 在点P从点A运动到点D的过程中,直线12与⊙F是否始终保持着上述的位置关系?请说明理由;
(3)在(2)条件下,当点P开始从点A出发,沿抛物线从左到右运动时,直线l2同时向下平移,垂足D的纵坐标yD以每秒3个单位长度速度变化,当直线l2与⊙F相交时,求t的取值范围.
【答案】
(1)
解:把点A(﹣1, ![]() ),B(2,0)代入抛物线11:y=ax2+bx+1中得:
),B(2,0)代入抛物线11:y=ax2+bx+1中得:
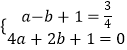 解得
解得 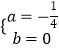 ,
,
∴y=﹣ ![]() x2+1 则对称轴为:直线x=0,顶点为(0,1)
x2+1 则对称轴为:直线x=0,顶点为(0,1)
(2)相切
(3)
解:设点P坐标(m,﹣ ![]() m2+1),则点F坐标(
m2+1),则点F坐标( ![]() m,﹣
m,﹣ ![]() m2+
m2+ ![]() ),
),
∵OP= ![]() =
= ![]() m2+1,
m2+1,
∴⊙F的半径= ![]() m2+
m2+ ![]() ,
,
∴直线y=﹣ ![]() m2+
m2+ ![]() ﹣(
﹣( ![]() m2+
m2+ ![]() )=﹣
)=﹣ ![]() m2与⊙F相切,
m2与⊙F相切,
∵t> ![]() 时,﹣
时,﹣ ![]() m2+1=1﹣2(t﹣
m2+1=1﹣2(t﹣ ![]() ),
),
∴﹣ ![]() m2=﹣2t+
m2=﹣2t+ ![]() ,
,
当1﹣3t=﹣2t+ ![]() 时直线l2与⊙F相切,解得t=
时直线l2与⊙F相切,解得t= ![]() ,
,
∴当0<t< ![]() 时,⊙F与直线l2相交
时,⊙F与直线l2相交
【解析】解:(2)①由题意1﹣ ![]() =2t解得t=
=2t解得t= ![]() ,
,
∴0≤t ![]() 时,yP=
时,yP= ![]() +2t,
+2t,
t> ![]() 时,yP=1﹣2(t﹣
时,yP=1﹣2(t﹣ ![]() )=
)= ![]() ﹣2t.
﹣2t.
②当点P在起点A处时,OA= ![]() =
= ![]() ,
,
∴⊙F的半径为 ![]() ,
,
∵点F坐标(﹣ ![]() ,
, ![]() ),
),
∴点F到直线y=1的距离为 ![]() ,
,
∴点F到直线y=1的距离等于⊙F的半径,
∴直线l2与⊙F相切,
所以答案是相切.
结论:在点P从点A运动到点D的过程中,直线12与⊙F始终保持相切.
理由:设点P坐标(m,﹣ ![]() m2+1),则点F坐标(
m2+1),则点F坐标( ![]() m,﹣
m,﹣ ![]() m2+
m2+ ![]() ),
),
∵OP= ![]() =
= ![]() m2+1,
m2+1,
∴⊙F的半径= ![]() m2+
m2+ ![]() ,
,
∵点F到直线y=1的距离为1﹣(﹣ ![]() m2+
m2+ ![]() )=
)= ![]() m2+
m2+ ![]() ,
,
∴点F到直线y=1的距离等于⊙F的半径,
∴在点P从点A运动到点D的过程中,直线12与⊙F始终保持相切.