题目内容
【题目】如图，正方形ABCD和正方形AEFG，边AE在边AB上，AB＝2AE＝2．将正方形AEFG绕点A逆时针旋转60°，BE的延长线交直线DG于点P ，旋转过程中点P运动的路线长为_______．
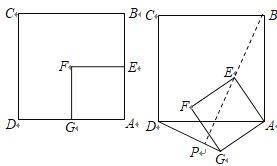
【答案】
【解析】试题解析：在△DAG和△BAE中
∴△DAG≌△BAE(SAS)，
∴∠ADG=∠ABE，
如图1，∵∠1=∠2，
∴
连接BD，则△BPD是以BD为斜边的直角三角形，
设BD的中点为O,连接OP,则
∴旋转过程中，点P运动的路线是以O为圆心，以OP为半径的一段弧，
如图2,当边AE在边AB上时,P与A重合,当
时,设AB的中点为M,连接ME,则
∴△AEM是等边三角形，
∴
∴
∴B、E.F三点共线，
∴P与F重合，
连接AF,可得△OFA是等边三角形, 
∴点P运动的路线长为： 
故答案为： 
练习册系列答案
相关题目
【题目】某学校计划购买若干台电脑，现从两家商场了解到同一种型号的电脑报价均为6000元，并且多买都有一定的优惠.各商场的优惠条件如下表所示：
商场 | 优惠条件 |
甲商场 | 第一台按原价收费，其余的每台优惠25% |
乙商场 | 每台优惠20% |
(1)设学校购买
台电脑，选择甲商场时，所需费用为
元，选择乙商场时，所需费用为
元，请分别求出，与之间的关系式.
(2)什么情况下，两家商场的收费相同？什么情况下，到甲商场购买更优惠？什么情况下，到乙商场购买更优惠？
(3)现在因为急需，计划从甲乙两商场一共买入10台电脑，已知甲商场的运费为每台50元，乙商场的运费为每台60元，设总运费为
元，从甲商场购买
台电脑，在甲商场的库存只有4台的情况下，怎样购买，总运费最少？最少运费是多少？
