题目内容
【题目】求证:角平分线上的点到这个角的两边的距离相等.
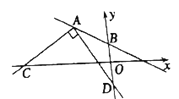
要求:(1)尺规作图:作∠AOB的角平分线,并在该角平分线上取点P,作PM⊥OA于点M,PN⊥OB于点N(不写作法,保留作图痕迹);
(2)以下是结合要证的命题和图形写出的已知,求证,请你完成证明过程.
已知:如图,OP平分∠AOB,PM⊥OA于点M,PN⊥OB于点N.
求证:PM=PN
证明:
【答案】详见解析
【解析】
(1)根据角平分线的作法得出即可;
(2)运用角角边定理先证△OPM≌△OPN,再根据全等三角形的性质得到PM=PN.
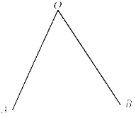
(1)如图所示:

证明:∵OP平分∠AOB,
∴∠AOP=∠BOP.
∵PM⊥OA,PN⊥OB
∴∠OMP=∠ONP=90°
在△OPM和△OPN中,

∴△OPM≌△OPN(AAS).
∴PM=PN.

【题目】某面粉加工厂加工的面粉,用每袋可装10g面粉的袋子装了200袋经过称重,质量超过标准质量10kg的用正数表示,质量低于标准质量10kg的用负数表示,结果记录如下
与标准质量的偏差(kg) | ﹣1.5 | ﹣1 | ﹣0.5 | 0 | 0.5 | 1 | 2 |
袋数(袋) | 40 | 30 | 10 | 25 | 40 | 20 | 35 |
(1)求这批面粉的总质量;
(2)如果100kg小麦加工80kg面粉,那么这批面粉是由多少千克小麦加工的?
【题目】某学校计划购买若干台电脑,现从两家商场了解到同一种型号的电脑报价均为6000元,并且多买都有一定的优惠.各商场的优惠条件如下表所示:
商场 | 优惠条件 |
甲商场 | 第一台按原价收费,其余的每台优惠25% |
乙商场 | 每台优惠20% |
(1)设学校购买![]() 台电脑,选择甲商场时,所需费用为
台电脑,选择甲商场时,所需费用为![]() 元,选择乙商场时,所需费用为
元,选择乙商场时,所需费用为![]() 元,请分别求出
元,请分别求出![]() ,
,![]() 与
与![]() 之间的关系式.
之间的关系式.
(2)什么情况下,两家商场的收费相同?什么情况下,到甲商场购买更优惠?什么情况下,到乙商场购买更优惠?
(3)现在因为急需,计划从甲乙两商场一共买入10台电脑,已知甲商场的运费为每台50元,乙商场的运费为每台60元,设总运费为![]() 元,从甲商场购买
元,从甲商场购买![]() 台电脑,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?
台电脑,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?