题目内容
【题目】已知:抛物线C1:y=﹣(x+m)2+m2(m>0),抛物线C2:y=(x﹣n)2+n2(n>0),称抛物线C1,C2互为派对抛物线,例如抛物线C1:y=﹣(x+1)2+1与抛物线C2:y=(x﹣![]() )2+2是派对抛物线,已知派对抛物线C1,C2的顶点分别为A,B,抛物线C1的对称轴交抛物线C2于C,抛物线C2的对称轴交抛物线C1与D.
)2+2是派对抛物线,已知派对抛物线C1,C2的顶点分别为A,B,抛物线C1的对称轴交抛物线C2于C,抛物线C2的对称轴交抛物线C1与D.
(1)已知抛物线①y=﹣x2﹣2x,②y=(x﹣3)2+3,③y=(x﹣![]() )2+2,④y=x2﹣x+
)2+2,④y=x2﹣x+![]() ,则抛物线①②③④中互为派对抛物线的是 (请在横线上填写抛物线的数字序号);
,则抛物线①②③④中互为派对抛物线的是 (请在横线上填写抛物线的数字序号);
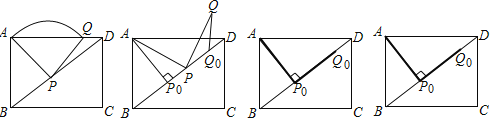
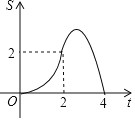
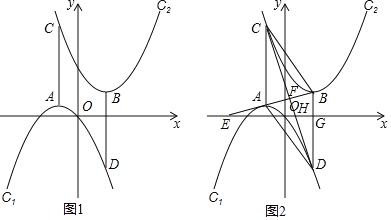
(2)如图1,当m=1,n=2时,证明AC=BD;
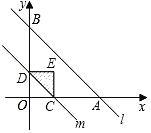
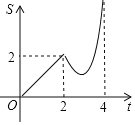
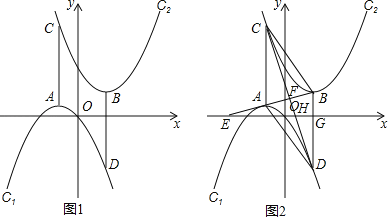
(3)如图2,连接AB,CD交于点F,延长BA交x轴的负半轴于点E,记BD交x轴于G,CD交x轴于点H,∠BEO=∠BDC.
①求证:四边形ACBD是菱形;
②若已知抛物线C2:y=(x﹣2)2+4,请求出m的值.
【答案】(1)①与③;①与④(2)证明见解析(3)①四边形ACBD是菱形②![]() -2
-2
【解析】
(1)先把四个解析式配成顶点式,然后根据派对抛物线的定义进行判断;
(2)利用抛物线C1:y=﹣(x+1)2+1,抛物线C2:y=(x﹣2)2+4得到A(﹣1,1),B(2,4),再计算出C(﹣1,13),D(2,﹣8),则AC=12,BD=12,于是可判断AC=BD;
(3)①先表示出A(﹣m,m2);B(n,n2),再表示出C(﹣m,m2+2mn+2n2),D(n,﹣2mn﹣n2),接着可计算出AC=BD=2mn+2n2,则可判断四边形ACBD为平行四边形,然后利用三角形内角和,由∠BEO=∠BDC得到∠EFH=∠DGH=90°,从而可判断四边形ACBD是菱形;②由抛物线C2:y=(x﹣2)2+4得到B(2,4),即n=2,则AC=BD=4m+8,再利用A(﹣m,m2)可表示出C(﹣m,m2+4m+8),所以BC2=(m+2)2+(m+2)4,然后利用BC=BD得(m+2)2+(m+2)4=(4m+8)2,最后利用m>0可求出m的值.
(1)①y=﹣x2﹣2x=﹣(x+1)2+12,②y=(x﹣3)2+3=(x﹣3)2+(![]() )2,③y=(x﹣
)2,③y=(x﹣![]() )2+(
)2+(![]() )2,④y=x2﹣x+
)2,④y=x2﹣x+![]() =(x﹣
=(x﹣![]() )2+(
)2+(![]() )2,
)2,
所以①与③互为派对抛物线;①与④互为派对抛物线;
故答案为①与③;①与④;
(2)证明:当m=1,n=2时,抛物线C1:y=﹣(x+1)2+1,抛物线C2:y=(x﹣2)2+4,
∴A(﹣1,1),B(2,4),
∵AC∥BD∥y轴,
∴点C的横坐标为﹣1,点D的横坐标为2,
当x=﹣1时,y=(x﹣2)2+4=13,则C(﹣1,13);
当x=2时,y=﹣(x+1)2+1=﹣8,则D(2,﹣8),
∴AC=13﹣1=12,BD=4﹣(﹣8)=12,
∴AC=BD;
(3)①抛物线C1:y=﹣(x+m)2+m2(m>0),则A(﹣m,m2);
抛物线C2:y=(x﹣n)2+n2(n>0),则B(n,n2);
当x=﹣m时,y=(x﹣n)2+n2=m2+2mn+2n2,则C(﹣m,m2+2mn+2n2);
当x=n时,y=﹣(x+m)2+m2=﹣2mn﹣n2,则D(n,﹣2mn﹣n2);
∴AC=m2+2mn+2n2﹣m2=2mn+2n2,BD=n2﹣(﹣2mn﹣n2)=2mn+2n2,
∴AC=BD;
∴四边形ACBD为平行四边形,
∵∠BEO=∠BDC,
而∠EHF=∠DHG,
∴∠EFH=∠DGH=90°,
∴AB⊥CD,
∴四边形ACBD是菱形;
②∵抛物线C2:y=(x﹣2)2+4,则B(2,4),
∴n=2,
∴AC=BD=2mn+2n2=4m+8,
而A(﹣m,m2),
∴C(﹣m,m2+4m+8),
∴BC2=(﹣m﹣2)2+(m2+4m+8﹣4)2=(m+2)2+(m+2)4,
∵四边形ACBD是菱形,
∴BC=BD,
∴(m+2)2+(m+2)4=(4m+8)2,
即(m+2)4=15(m+2)2,
∵m>0,
∴(m+2)2=15,
∴m+2=![]() ,
,
∴m=![]() ﹣2.
﹣2.

 阅读快车系列答案
阅读快车系列答案【题目】如图,矩形ABCD中,AB=6,AD=4![]() ,点E是BC的中点,点F在AB上,FB=2,P是矩形上一动点.若点P从点F出发,沿F→A→D→C的路线运动,当∠FPE=30°时,FP的长为_____.
,点E是BC的中点,点F在AB上,FB=2,P是矩形上一动点.若点P从点F出发,沿F→A→D→C的路线运动,当∠FPE=30°时,FP的长为_____.

【题目】九(1)班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类别,每位同学仅选一项.根据调査结果绘制了不完整的频数分布表和扇形统计图.
类别 | 频数(人数) | 频率 |
小说 | a | 0.5 |
戏剧 | 4 | |
散文 | 10 | 0.25 |
其他 | 6 | |
合计 | b | 1 |
根据图表提供的信息,回答下列问题:
(1)直接写出:a= .b= m= ;
(2)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从中任意选出2名同学参加学校的戏剧社团,请求选取的2人恰好是甲和乙的概率.