题目内容
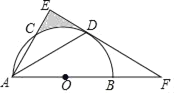
【题目】如图,矩形ABCD中,AB=6,AD=4![]() ,点E是BC的中点,点F在AB上,FB=2,P是矩形上一动点.若点P从点F出发,沿F→A→D→C的路线运动,当∠FPE=30°时,FP的长为_____.
,点E是BC的中点,点F在AB上,FB=2,P是矩形上一动点.若点P从点F出发,沿F→A→D→C的路线运动,当∠FPE=30°时,FP的长为_____.

【答案】4或8或4![]()
【解析】
如图,连接DF,AE,DE,取DF的中点O,连接OA、OE.以O为圆心画⊙O交CD于P3.只要证明∠EP1F=∠FP2F=∠FP3E=30°,即可推出FP1=4,FP2=8,FP3=4![]() 解决问题.
解决问题.
如图,连接DF,AE,DE,取DF的中点O,连接OA、OE.以O为圆心画⊙O交CD于P3.
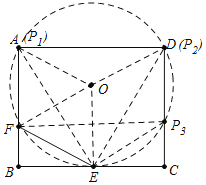
∵四边形ABCD是矩形,
∴∠BAD=∠B=90°,
∵BF=2,BE=2![]() ,AF=4,AD=4
,AF=4,AD=4![]() ,
,
∴tan∠FEB=tan∠ADF=![]() ,
,
∴∠ADF=∠FEB=30°,
易知EF=OF=OD=4,
∴△OEF是等边三角形,
∴∠EP1F=∠FP2F=∠FP3E=30°,
∴FP1=4,FP2=8,FP3=4![]() ,
,
故答案为4或8或4![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目