题目内容
【题目】反比例函数y=![]() (1≤x≤8)的图象记为曲线C1,将C1沿y轴翻折,得到曲线C2,直线y=-x+b 与C1 ,C2一共只有两个公共点,则b的取值范围是______________________.
(1≤x≤8)的图象记为曲线C1,将C1沿y轴翻折,得到曲线C2,直线y=-x+b 与C1 ,C2一共只有两个公共点,则b的取值范围是______________________.
【答案】![]()
【解析】分析:作出大致图象,分两种情况讨论:①当直线y=-x+b与反比例函数y=![]() 只有一个交点时,解方程组得b=
只有一个交点时,解方程组得b=![]() ;②当直线y=-x+b过(-1,8)时,直线刚好与C1 ,C2有三个公共点,由此得到b的值,把此直线往上平移,直线与C2没有公共点,与C1有两个公共点,直到直线过(1,8),解得此时b的值,即可得出结论.
;②当直线y=-x+b过(-1,8)时,直线刚好与C1 ,C2有三个公共点,由此得到b的值,把此直线往上平移,直线与C2没有公共点,与C1有两个公共点,直到直线过(1,8),解得此时b的值,即可得出结论.
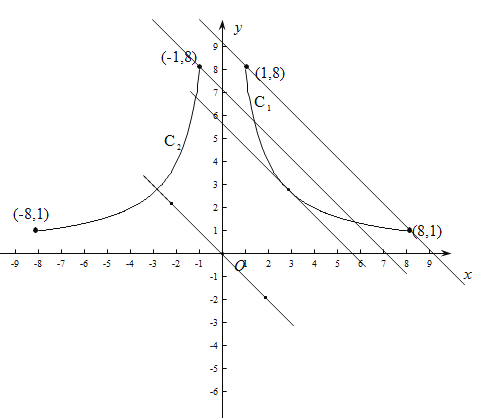
详解:如图,直线y=-x+b与直线l:y=-x平行.分两种情况讨论:
①当直线y=-x+b与反比例函数y=![]() 只有一个交点时,解方程组
只有一个交点时,解方程组 得:
得:![]() ,∴
,∴![]() ,∴△=b2-32=0,解得:b=±
,∴△=b2-32=0,解得:b=±![]() (负数舍去),∴b=
(负数舍去),∴b=![]() ,∴当b=
,∴当b=![]() ,直线y=-x+b与C1 ,C2一共只有两个公共点.
,直线y=-x+b与C1 ,C2一共只有两个公共点.
②当直线y=-x+b过(-1,8)时,直线刚好与C1 ,C2有三个公共点,此时8=1+b,解得:b=7,此时直线为y=-x+7,把此直线往上平移,直线与C2没有公共点,与C1有两个公共点,直到直线过(1,8),此时8=-1+b,解得:b=9.∴7<b≤9.
综上所述:b的取值范围是:b=![]() 或7<b≤9.
或7<b≤9.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目