Question

【题目】如图①所示，已知MN∥PQ，点B在MN上，点C在PQ上，点A在点B的左侧，点D在点C的右侧，∠ADC，∠ABC的平分线相交于点E(不与B，D点重合)，∠CBN＝110°.

(1)若∠ADQ＝140°，写出∠BED的度数 (直接写出结果即可)；

(2)若∠ADQ＝m°，将线段AD沿DC方向平移，使点D移动到点C的左侧，其他条件不变，如图②所示，求∠BED的度数(用含m的式子表示)．

Answer 1

【答案】(1)55°；(2) ∠BED＝215°－m°.

【解析】

（1）过点E作EF∥PQ，根据邻补角的定义求出∠CBM=70°，∠ADP=40°，再根据角平分线的定义求出∠EBM=35°，∠EDP=20°，再根据两直线平行，内错角相等可得∠DEF=∠EDP，∠FEB=∠EBM，然后根据∠BED=∠DEF+∠FEB代入数据计算即可得解；

（2）过点E作EF∥PQ，根据邻补角的定义求出∠CBM=70°，∠ADP=m°，再根据角平分线的定义求出∠EBM=35°，∠EDP=m°，再根据两直线平行，内错角相等可得∠DEF=∠EDP，∠FEB=∠EBM，然后根据∠BED=∠DEF+∠FEB代入数据计算即可得解．

（1）如图（1），过点E作EF∥PQ．

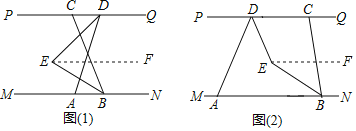
∵∠CBN=110°，∠ADQ=140°，

∴∠CBM=70°，∠ADP=40°．

∵∠CDE=∠ADE，∠ABE=∠CBE，

∴∠EBM=35°，∠EDP=20°．

∵EF∥PQ，

∴∠DEF=∠EDP=20°．

∵EF∥PQ，MN∥PQ，

∴EF∥MN，

∴∠FEB=∠EBM=35°，

∴∠BED=∠DEF+∠FEB=20°+35°=55°；

故答案为：55°

（2）如图（2），过点E作EF∥PQ．

∵∠CBN=110°，

∴∠CBM=70°．

∵∠CDE=∠ADE，∠ABE=∠CBE，

∴∠EBM=35°，∠EDQ=m°．

∵EF∥PQ，

∴∠DEF=180°-∠EDQ=180°-m°．

∵EF∥PQ，MN∥PQ，

∴EF∥MN，

∴∠FEB=∠EBM=35°，

∴∠BED=∠DEF+∠FEB=180°-m°+35°=215°-m°．