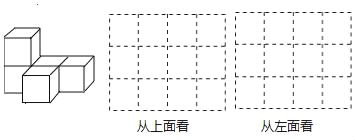
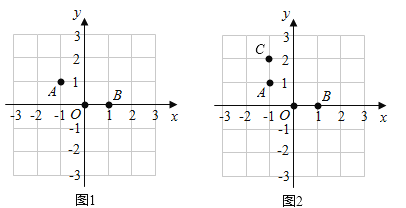
题目内容
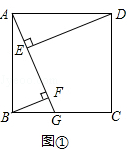
【题目】如图,在梯形![]() ,
,![]() ,过点
,过点![]() ,垂足为
,垂足为![]() ,并延长
,并延长![]() ,使
,使![]() ,联结
,联结![]() .
.
(1)求证:四边形![]() 是平行四边形。
是平行四边形。
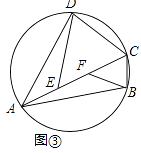
(2)联结![]() ,如果
,如果![]()

【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)连接BD,证△ABC≌△DCB,得∠ACB=∠DBC.由中垂线性质得BD=BF,∠DBC=∠FBC,
再证得AC=BF,∠ACB=∠CBF,由AC,BF平行且相等可证得四边形![]() 是平行四边形.
是平行四边形.
(2)由BF=DF=BD证得三角形BDF是等边三角形,可得![]() ,再由平行线性质和等腰三角形性质证
,再由平行线性质和等腰三角形性质证![]() ,可得
,可得![]() ,由(1)可得
,由(1)可得![]()
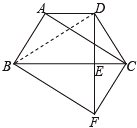
∵梯形ABCD中,AD∥BC,AB=DC,
∴AC=BD,
∵△ABC和△DCB中,AB=DC,AC=BD,BC=CB,
∴△ABC≌△DCB.
∴∠ACB=∠DBC.
又∵DE⊥BC,EF=DE,
∴BD=BF,∠DBC=∠FBC,
∴AC=BF,∠ACB=∠CBF,
∴AC∥BF,
∴四边形ABFC是平行四边形;
(2)
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() 四边形ABFC是平行四边形
四边形ABFC是平行四边形
![]()

练习册系列答案
相关题目
【题目】某社区为了进一步提高居民珍惜谁、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每季度的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图和表: 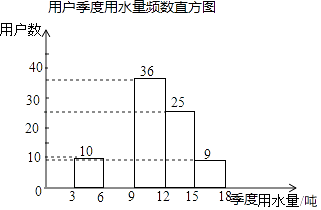
用户季度用水量频数分布表
平均用水量(吨) | 频数 | 频率 |
3<x≤6 | 10 | 0.1 |
6<x≤9 | m | 0.2 |
9<x≤12 | 36 | 0.36 |
12<x≤15 | 25 | n |
15<x≤18 | 9 | 0.09 |
请根据上面的统计图表,解答下列问题:
(1)在频数分布表中:m= , n=;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本季度水量定为每户每季度9吨,不超过基本季度用水量的部分享受基本价格,超出基本季度用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?