äãá¢áÖàï
Àƒäãá¢À¢àÓë¥È˜øÝüÔ ![]() 1Ȥy=kx+b ñøÝÞ§£ x øÃÀÂy øÃÆÖçÐ B(4Ș0)ÀÂNȘøÝüÔ
1Ȥy=kx+b ñøÝÞ§£ x øÃÀÂy øÃÆÖçÐ B(4Ș0)ÀÂNȘøÝüÔ![]() 2:y=2x-1ñøÝÞ§£ x øÃÀÂy øÃÆÖçÐ MÀÂAȘ
2:y=2x-1ñøÝÞ§£ x øÃÀÂy øÃÆÖçÐ MÀÂAȘ![]() 1Ș
1Ș![]() 2 §£çÐ P çáæ½Ýõ(mȘ2)ȘúŠ¡ªƒïë¥üµùªäÿˋçáÅéü§ãÇÞüôêÅöòäãȤ
2 §£çÐ P çáæ½Ýõ(mȘ2)ȘúŠ¡ªƒïë¥üµùªäÿˋçáÅéü§ãÇÞüôêÅöòäãȤ

(1)çÝ x òÝȘkx+bÀï2x-1È£
(2)ý£çàò§ k![]() +bÈ¥0 çá§ã¥₤òú È£
+bÈ¥0 çá§ã¥₤òú È£
(3)åÖó§ûÌáÖòúñþÇÌåÖØ£çÐ HȘò¿çûØåAȘBȘPȘHùáçÐæÕ°èçáùáÝÔÅöòúó§ÅÅùáÝÔÅöÈÛà¶ÇÌåÖȘøݧÆÅÇ°—çÐ H çáæ½ÝõȘà¶ý£ÇÌåÖȘùçû¼âÚÆèÈÛ
ÀƒÇÞ¯¡À¢(1)![]() È£ (2)
È£ (2)![]() È£ (3)ÇÌåÖȘçÐHçáæ½Ýõöˆ(
È£ (3)ÇÌåÖȘçÐHçáæ½Ýõöˆ(![]() Ș
Ș![]() )£·(
)£·(![]() Ș
Ș![]() )£·(
)£·(![]() Ș
Ș![]() )
)
Àƒ§ãö—À¢
(1)üàúµçûçÐPçáæ½ÝõȘ¡ªƒï¤₤ò»ë¥üµÈ˜¥Ç¢èúµ§ãÈ£
(2)¡ªƒï¤₤ò»ë¥üµÈ˜¥Ç¢èúµ§ãÈ£
(3)èÒçÐHçáæ½Ýõöˆ(aȘn)ȘñøABöˆÑå§úüÔÀÂAPöˆÑå§úüÔ¥¯BPöˆÑå§úüÔà»øøúÕ¢—Șâ«Æûó§ÅÅùáÝÔÅöçáÅåøò(Ñå§úüÔ£ËüÁó§ñø)¢èúµ°—çÐHçáæ½ÝõÈÛ
(1)ÀÔçÐP(mȘ2)åÖøÝüÔ![]() 2:
2:![]() èüȘ
èüȘ
êŸ![]() Șå·
Șå·![]() Ș
Ș
ÀÁçÐPçáæ½Ýõöˆ(![]() Ș2)Ș
Ș2)Ș
¿Üýš¤₤ò»ë¥üµÈ˜çÝ![]() òÝȘøÝüÔ
òÝȘøÝüÔ ![]() 1åÖøÝüÔ
1åÖøÝüÔ![]() 2çáèüñ§È˜
2çáèüñ§È˜
ÀÁçÝ![]() òÝȘ
òÝȘ![]() È£
È£
(2)øÝüÔ ![]() 1Ȥ
1Ȥ![]() ñøÝÞ§£
ñøÝÞ§£![]() øÃÆÖçÐ B(4Ș0)Ș
øÃÆÖçÐ B(4Ș0)Ș
¿Üýš¤₤ò»ë¥üµÈ˜çÝ![]() òÝȘøÝüÔ
òÝȘøÝüÔ ![]() 1åÖ
1åÖ![]() øÃçáüôñ§È˜
øÃçáüôñ§È˜
ÀÁý£çàò§![]() çá§ã¥₤öˆÈ¤
çá§ã¥₤öˆÈ¤![]() È£
È£
(3)ÇÌåÖȘèÒçÐHçáæ½Ýõöˆ(aȘn)Ș
êŸ![]() Șå·
Șå·![]() Ș
Ș
ÀÁçÐAçáæ½Ýõöˆ(0Ș![]() )Ș
)Ș
ÀÔçÐBçáæ½Ýõöˆ(4Ș0)ȘçÐPçáæ½Ýõöˆ(![]() Ș2)Ș
Ș2)Ș
ñøà»øøúÕ¢—¢¥ôúȘàÓë¥ùªòƒÈ¤
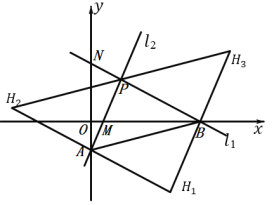
ÂìçÝABöˆÑå§úüÔòÝȘ
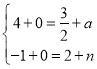
§ãçûȤ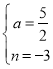 Ș
Ș
ÀÁçÐ![]() çáæ½Ýõöˆ(
çáæ½Ýõöˆ(![]() Ș
Ș![]() )ȣ
)È£
ÂÖçÝAPöˆÑå§úüÔòÝȘ
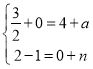 Ș
Ș
§ãçûȤ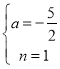 Ș
Ș
ÀÁçÐ![]() çáæ½Ýõöˆ(
çáæ½Ýõöˆ(![]() Ș
Ș![]() )ȣ
)È£
ÂÜçÝBPöˆÑå§úüÔòÝȘ
 Ș
Ș
§ãçûȤ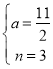 Ș
Ș
ÀÁçÐ![]() çáæ½Ýõöˆ(
çáæ½Ýõöˆ(![]() Ș
Ș![]() )ȣ
)È£
æÜèüùªò—ȤåÖó§ûÌøݧúæ½ÝõüçøÅÇÌåÖçÐHȘò¿ØåçÐAȘBȘPȘHöˆÑËçÐçáùáÝÔÅöòúó§ÅÅùáÝÔÅöȘçÐHçáæ½Ýõöˆ(![]() Ș
Ș![]() )£·(
)£·(![]() Ș
Ș![]() )£·(
)£·(![]() Ș
Ș![]() ) ÈÛ
) ÈÛ