题目内容
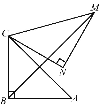
【题目】如图，将平行四边形 ABCD 沿对角线 BD 折叠，使点 A 落在A′处，若∠1＝∠2＝50°，则∠A′的度数为（ ）
A.100°B.105°C.110°D.115°
【答案】B
【解析】
由平行四边形的性质和折叠的性质，得出∠ADB=∠BDG=∠DBG，由三角形的外角性质求出∠1=∠BDG+∠DBG=50°，再由三角形内角和定理求出∠A，即可得到结果．
∵AD∥BC，
∴∠ADB=∠DBG，
由折叠可得∠ADB=∠BDG，
∴∠DBG=∠BDG，
又∵∠1=∠BDG+∠DBG=50°，
∴∠ADB=∠BDG=25°，
又∵∠2=50°，
∴△ABD中，∠A=180°-∠2-∠ADB =105°，
∴∠A'=∠A=105°，
故选：B．
练习册系列答案
名校课堂系列答案
相关题目
