题目内容
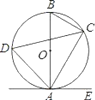
【题目】如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
(1)求∠ABC的度数;
(2)求证:AE是⊙O的切线;
(3)当BC=4时,求劣弧AC的长.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】试题分析:(1)根据圆周角定理,即可求得∠ABC的度数;
(2)由AB是⊙O的直径,根据半圆(或直径)所对的圆周角是直角,即可得∠ACB=90°,又由∠BAC=30°,易求得∠BAE=90°,则可得AE是⊙O的切线;
(3)首先连接OC,易得△OBC是等边三角形,则可得∠AOC=120°,由弧长公式,即可求得劣弧AC的长.
试题解析:(1)∵∠ABC与∠D都是弧AC所对的圆周角,∴∠ABC=∠D=60°;
(2)∵AB是⊙O的直径,∴∠ACB=90°,∴∠BAC=30°,∴∠BAE=∠BAC+∠EAC=30°+60°=90°,即BA⊥AE,∴AE是⊙O的切线;
(3)如图,连接OC,∵∠ABC=60°,∴∠AOC=120°,∴劣弧AC的长为![]() =
= ![]() .
.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目





