题目内容
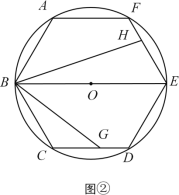
【题目】如图，已知圆O是正六边形ABCDEF外接圆，直径BE=8，点G、H分别在射线CD、EF上（点G不与点C、D重合），且∠GBH=60°，设CG=x，EH=y．
（1）如图①，当直线BG经过弧CD的中点Q时，求∠CBG的度数；
（2）如图②，当点G在边CD上时，试写出y关于x的函数关系式，并写出x的取值范围；
（3）联结AH、EG，如果△AFH与△DEG相似，求CG的长．
【答案】（1）∠CBG=15°；（2）
（
）；（3）CG的长为12
【解析】
（1）连接OQ，根据正六边形的特点和内角和求出∠EBC =60°，然后通过弧之间的关系得出∠BOQ=∠EOQ=90°，又因为BO=OQ，得出∠OBQ=∠BQO=45°，最后利用∠CBG=∠EBC-∠OBQ即可求出答案；
（2）在BE上截取EM=HE，连接HM，首先根据正六边形的性质得出
是等边三角形，则有EM=HE=HM=y，∠HME=60°，从而有∠C=∠HMB=120°，然后通过等量代换得出∠GBC=∠HBE，由此可证明△BCG∽△BMH，则有
，即
，则y关于x的函数关系式可求，因为点Q在边CD上，则x的取值范围可求；
（3）分两种情况：①当点G在边CD上时：又分当
时和当
时两种情况；②当点G在CD的延长线上时，同样分当时和当时两种情况，分别建立方程求解并检验即可得出答案．
解：（1）如图，连接OQ．
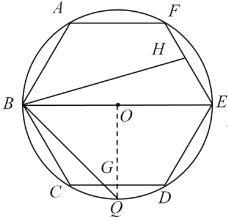
∵六边形ABCDEF是正六边形，
∴BC=DE，∠ABC=120°．
∴
，∠EBC=
∠ABC=60°．
∵点Q是
的中点，
∴
．
∴
，
即
．
∴∠BOQ=∠EOQ，
又∵∠BOQ+∠EOQ=180°，
∴∠BOQ=∠EOQ=90°．
又∵BO=OQ，
∴∠OBQ=∠BQO=45°，
∴∠CBG=60°
45°=15°．
（2）如图，在BE上截取EM=HE，连接HM．
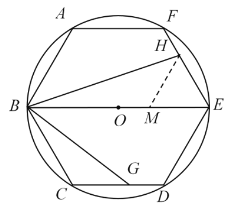
∵六边形ABCDEF是正六边形，直径BE=8，
∴BO=OE=BC=4，∠C=∠FED=120°，
∴∠FEB=∠FED=60°．
∵EM=HE，
∴是等边三角形，
∴EM=HE=HM=y，∠HME=60°，
∴∠C=∠HMB=120°．
∵∠EBC=∠GBH=60°，
∴∠EBC∠GBE=∠GBH∠GBE，
即∠GBC=∠HBE．
∴△BCG∽△BMH，
∴．
又∵CG= x，BE=8，BC=4，
∴，
∴y与x的函数关系式为（）．
（3）如图，当点G在边CD上时．
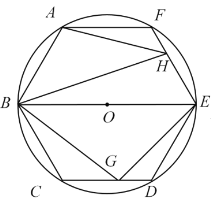
由于△AFH∽△EDG，且∠CDE=∠AFE=120°，
① 当时，
∵AF=ED，
∴FH=DG，
∴
，
即：
，解分式方程得
．
经检验是原方程的解，但不符合题意舍去．
② 当时，
即：
，解分式方程得
．
经检验是原方程的解，但不符合题意舍去．
如图，当点G在CD的延长线上时．
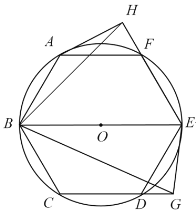
由于△AFH∽△EDG，且∠EDG=∠AFH=60°，
① 当时，
∵AF=ED，
∴FH=DG
∴，
即：，解分式方程得．
经检验是原方程的解，但不符合题意舍去．
② 当时，
即：
，解分式方程得．
经检验是原方程的解，且符合题意．
∴综上所述，如果△AFH与△DEG相似，那么CG的长为12．
