题目内容
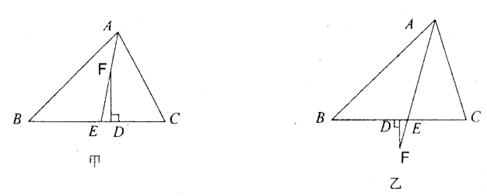
已知,如图甲,在△ABC中,AE平分∠BAC(∠C>∠B),F为AE上一点,且FD⊥BC于D。
(1)试说明:∠EFD=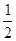 (∠C-∠B);
(∠C-∠B);
(2)当F在AE的延长线上时,如图乙,其余条件不变,(1)中的结论还成立吗?请说明理由。

(1)试说明:∠EFD=
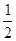 (∠C-∠B);
(∠C-∠B);(2)当F在AE的延长线上时,如图乙,其余条件不变,(1)中的结论还成立吗?请说明理由。
(1)通过角的负余证明。(2)成立
试题分析:(1)证明:∵FD⊥EC∴∠EFD=90°-∠FEC
∴∠FEC=∠B+∠BAE
又∵AE平分∠BAC
∴∠BAE=
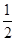 ∠BAC=
∠BAC=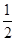 (180°-∠B-∠C)=90°-
(180°-∠B-∠C)=90°-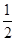 (∠B+∠C)
(∠B+∠C)则∠EFD=90°
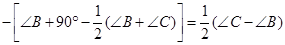
(2)∵AE平分∠BAC,∴∠BAE=
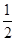 ∠BAC.
∠BAC.∵∠BAC=180°-(∠B+∠C);
∴∠BAE=
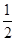 [180°-(∠B+∠C)];
[180°-(∠B+∠C)];∴∠FED=∠B+∠BAE=∠B+
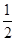 [180°-(∠B+∠C)]=90°+
[180°-(∠B+∠C)]=90°+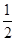 (∠B-∠C).
(∠B-∠C).又∵FD⊥BC,∴∠FDE=90°;
∴∠EFD=90°-[90°+
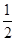 (∠B-∠C)=
(∠B-∠C)=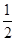 (∠C-∠B)].
(∠C-∠B)].点评:此题主要考查了角平分线的性质、三角形内角和定理和直角三角形的性质,命题时经常将多个知识点联系在一起进行考查,这样更能训练学生的解题能力.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 ,AC平分
,AC平分 ,求
,求 的度数。
的度数。



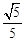


 点出发,要到距离
点出发,要到距离
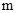 的
的 地去,先沿北偏东
地去,先沿北偏东 方向到达
方向到达 地,然后再沿北偏西
地,然后再沿北偏西 方向走了
方向走了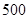

 方向上
方向上 方向上
方向上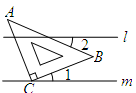
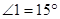 ,
,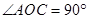 ,点B、O、D在同一直线上,则
,点B、O、D在同一直线上,则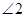 的度数为 .
的度数为 .