题目内容
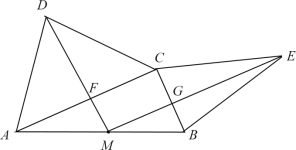
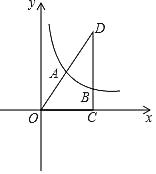
【题目】如图,在⊙O中,AB是的直径,PA与⊙O 相切于点A,点C在⊙O 上,且PC=PA,
(1)求证PC是⊙O的切线;
(2)过点C作CD⊥AB于点E,交⊙O于点D,若CD=PA=2![]() ,
,
①求图中阴影部分面积;
②连接AC,若△PAC的内切圆圆心为I,则线段IE的长为 .

【答案】(1)详见解析;(2)①S阴影=![]() . ②
. ②![]() .
.
【解析】
(1)连接OCOP,证明△PCO≌△PAO,即可解答
(2)①作CM⊥AP于点M,得到△PCA是等边三角形.然后在Rt△COE中得到OC=2.即可解答 .
②根据题意求出CH=![]() AH=3,由I为正△PAC的内心,即可求出解答 .
AH=3,由I为正△PAC的内心,即可求出解答 .
(1)证明:连接OCOP,
∵点C在⊙O上,
∴OC为半径.
∵PA与⊙O相切于点A,
∴OA⊥PA.
∴∠PAO=90°.
∵OC=OA,
OP=OP,
PC=PA,
∴△PCO≌△PAO.
∴∠PCO=∠PAO=90°.
∴PC⊥OC.
∴PC是⊙O的切线.
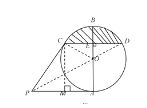
(2)①作CM⊥AP于点M,
∵CD⊥AB,
∴CE=DE=![]() ,∠CEA=90°.
,∠CEA=90°.
∴四边形CMAE是矩形.
∴AM=![]() .
.
∴PM=AM.
∴PC=AC.
∵PC=PA,
∴△PCA是等边三角形.
∴∠PAC=60°.
∴∠CAB=30°.
∴∠COE=60°.
∴∠COD=120°.
在Rt△COE中,
sin60°=![]() ,
,
∴OC=2.
∴S阴影=![]() π-
π-![]() .
.
②∵AP=2![]() ,AH=CE=
,AH=CE=![]()
∴CH=![]() AH=3
AH=3
又∵I为正△PAC的内心
∴CI=![]() CH=2
CH=2
∴IE=![]() =
=![]() =
=![]()

【题目】为了庆祝“五四”青年节,我市某中学举行了书法比赛,赛后随机抽查部分参赛同学成绩(满分为100分),并制作成图表如下
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | m | 0.45 |
80≤x<90 | 60 | n |
90≤x≤100 | 20 | 0.1 |
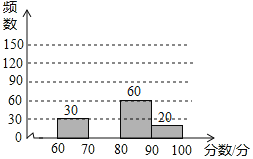
请根据以上图表提供的信息,解答下列问题:
(1)这次随机抽查了 名学生;表中的数m= ,n= ;
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是 ;
(4)全校共有600名学生参加比赛,估计该校成绩不低于80分的学生有多少人?