题目内容
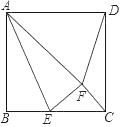
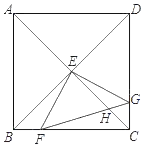
【题目】如图,正方形ABCD的边长为![]() ,对角线AC和BD交于点E,点F是BC边上一动点(不与点B,C重合),过点E作EF的垂线交CD于点G,连接FG交EC于点H.设BF=x,CH=y,则y与x的函数关系的图象大致是( )
,对角线AC和BD交于点E,点F是BC边上一动点(不与点B,C重合),过点E作EF的垂线交CD于点G,连接FG交EC于点H.设BF=x,CH=y,则y与x的函数关系的图象大致是( )
A. 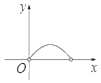 B.
B. 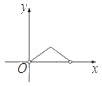 C.
C. 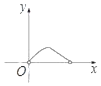 D.
D. 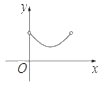
【答案】A
【解析】
证明△BEF∽△CFH,可得![]()
,由此构建函数关系式即可解决问题.
∵四边形ABCD是正方形,
∴∠EBF=∠ECG=45°,AC⊥BD,EB=EC,
∵EF⊥EG,
∴∠BEC=∠FEG=90°,
∴∠BEF=∠CEG,
∴△BEF≌△CEG(ASA),
∴EF=EG,
∴∠EFG=45°,
∵∠EFC=45°+∠CFH=45°+∠BEF,
∴∠CFH=∠BEF,
∴△BEF∽△CFH,
∴![]() ,
,
∴![]() ,
,
∴y=![]() ,
,
故选:A.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目