题目内容
如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(6,0),(6,8).动点M、N分别从O、B同时出发,以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点N作NP⊥BC,交AC于P,连接MP.已知动点运动了x秒.(1)P点的坐标为多少;(用含x的代数式表示)
(2)试求△MPA面积的最大值,并求此时x的值;
(3)请你探索:当x为何值时,△MPA是一个等腰三角形?你发现了几种情况?写出你的研究成果.
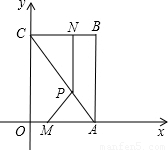
【答案】分析:(1)P点的横坐标与N点的横坐标相同,求出CN的长即可得出P点的横坐标,然后通过求直线AC的函数解析式来得出P点的纵坐标,由此可求出P点的坐标;
(2)可通过求△MPA的面积和x的函数关系式来得出△MPA的面积最大值及对应的x的值.
△MPA中,MA=OA-OM,而MA边上的高就是P点的纵坐标,由此可根据三角形的面积计算公式求出S与x的函数关系式,进而根据函数的性质得出S的最大值和对应的x的值;
(3)可分三种情况进行讨论:
①MP=AP时,延长NP交x轴于Q,则有PQ⊥OA,那么此时有AQ=BN= MA,由此可求出x的值.
MA,由此可求出x的值.
②当MP=AM时,可根据MP、AM的不同表达式得出一个关于x的方程即可求出x的值.
③当MP=MA时,可在直角三角形PMQ中,根据勾股定理求出x的值.
综上所述可得出符合条件的x的值.
解答: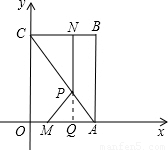 解:(1)由题意可知C(0,8),又A(6,0),
解:(1)由题意可知C(0,8),又A(6,0),
所以直线AC解析式为:y=- x+8,
x+8,
因为P点的横坐标与N点的横坐标相同为6-x,代入直线AC中得y= ,
,
所以P点坐标为(6-x, x);
x);
(2)设△MPA的面积为S,在△MPA中,MA=6-x,MA边上的高为 x,
x,
其中,0≤x<6,
∴S= (6-x)×
(6-x)× x=
x= (-x2+6x)=-
(-x2+6x)=- (x-3)2+6,
(x-3)2+6,
∴S的最大值为6,此时x=3;
(3)延长NP交x轴于Q,则有PQ⊥OA
①若MP=PA,
∵PQ⊥MA,
∴MQ=QA=x,
∴3x=6,
∴x=2;
②若MP=MA,则MQ=6-2x,PQ= x,PM=MA=6-x,
x,PM=MA=6-x,
在Rt△PMQ中,
∵PM2=MQ2+PQ2,
∴(6-x)2=(6-2x)2+( x)2,
x)2,
∴x= ;
;
③若PA=AM,
∵PA= x,AM=6-x,
x,AM=6-x,
∴ x=6-x,
x=6-x,
∴x= ,
,
综上所述,x=2,或x=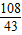 ,或x=
,或x= .
.
点评:本题着重考查了二次函数的应用、矩形的性质、图形面积的求法等知识点,考查学生分类讨论,数形结合的数学思想方法.
(2)可通过求△MPA的面积和x的函数关系式来得出△MPA的面积最大值及对应的x的值.
△MPA中,MA=OA-OM,而MA边上的高就是P点的纵坐标,由此可根据三角形的面积计算公式求出S与x的函数关系式,进而根据函数的性质得出S的最大值和对应的x的值;
(3)可分三种情况进行讨论:
①MP=AP时,延长NP交x轴于Q,则有PQ⊥OA,那么此时有AQ=BN=
 MA,由此可求出x的值.
MA,由此可求出x的值.②当MP=AM时,可根据MP、AM的不同表达式得出一个关于x的方程即可求出x的值.
③当MP=MA时,可在直角三角形PMQ中,根据勾股定理求出x的值.
综上所述可得出符合条件的x的值.
解答:
 解:(1)由题意可知C(0,8),又A(6,0),
解:(1)由题意可知C(0,8),又A(6,0),所以直线AC解析式为:y=-
 x+8,
x+8,因为P点的横坐标与N点的横坐标相同为6-x,代入直线AC中得y=
 ,
,所以P点坐标为(6-x,
 x);
x);(2)设△MPA的面积为S,在△MPA中,MA=6-x,MA边上的高为
 x,
x,其中,0≤x<6,
∴S=
 (6-x)×
(6-x)× x=
x= (-x2+6x)=-
(-x2+6x)=- (x-3)2+6,
(x-3)2+6,∴S的最大值为6,此时x=3;
(3)延长NP交x轴于Q,则有PQ⊥OA
①若MP=PA,
∵PQ⊥MA,
∴MQ=QA=x,
∴3x=6,
∴x=2;
②若MP=MA,则MQ=6-2x,PQ=
 x,PM=MA=6-x,
x,PM=MA=6-x,在Rt△PMQ中,
∵PM2=MQ2+PQ2,
∴(6-x)2=(6-2x)2+(
 x)2,
x)2,∴x=
 ;
;③若PA=AM,
∵PA=
 x,AM=6-x,
x,AM=6-x,∴
 x=6-x,
x=6-x,∴x=
 ,
,综上所述,x=2,或x=
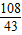 ,或x=
,或x= .
.点评:本题着重考查了二次函数的应用、矩形的性质、图形面积的求法等知识点,考查学生分类讨论,数形结合的数学思想方法.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
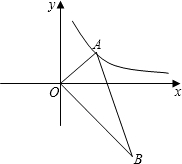 如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线
如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线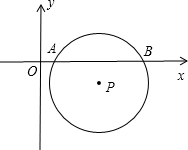 =2
=2 如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
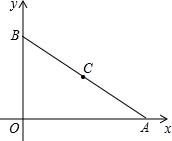 如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.
如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.