ЬтФПФкШн
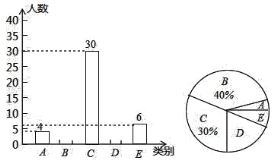
ЁОЬтФПЁПШчЭМЃЌвбжЊЫФБпаЮ![]() ЪЧЦНааЫФБпаЮЃЌЕу
ЪЧЦНааЫФБпаЮЃЌЕу![]() КЭ
КЭ![]() дк
дк![]() жсЩЯЃЌЧв
жсЩЯЃЌЧв![]() ЮЊзјБъдЕуЃЌЕу
ЮЊзјБъдЕуЃЌЕу![]() ЃЌКЭЕу
ЃЌКЭЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ВЂбгГЄНЛ
ВЂбгГЄНЛ![]() жсгкЕу
жсгкЕу![]() ЃЎ
ЃЎ
(1)ЧѓжБЯп![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
(2)ШєЕу![]() Дг
Дг![]() ГіЗЂвд2ИіЕЅЮЛ/УыЕФЫйЖШби
ГіЗЂвд2ИіЕЅЮЛ/УыЕФЫйЖШби![]() жсЯђгвдЫЖЏЃЌЭЌЪБЕу
жсЯђгвдЫЖЏЃЌЭЌЪБЕу![]() Дг
Дг![]() ГіЗЂЃЌвд1ИіЕЅЮЛ/УыЕФЫйЖШби
ГіЗЂЃЌвд1ИіЕЅЮЛ/УыЕФЫйЖШби![]() жсЯђзѓдЫЖЏЃЌЙ§Еу
жсЯђзѓдЫЖЏЃЌЙ§Еу![]() ЃЌ
ЃЌ![]() ЗжБ№зї
ЗжБ№зї![]() жсЕФДЙЯпНЛЩфЯп
жсЕФДЙЯпНЛЩфЯп![]() КЭЩфЯп
КЭЩфЯп![]() ЗжБ№гкЕу
ЗжБ№гкЕу![]() ЃЌ
ЃЌ![]() ЃЌЧыВТЯыЫФБпаЮ
ЃЌЧыВТЯыЫФБпаЮ![]() ЕФаЮзДЃЌ(Еу
ЕФаЮзДЃЌ(Еу![]() ЃЌ
ЃЌ![]() жиКЯГ§Эт)ЃЌВЂжЄУїФуЕФНсТлЃЎ
жиКЯГ§Эт)ЃЌВЂжЄУїФуЕФНсТлЃЎ
(3)дк(2)ЕФЬѕМўЯТЃЌЕБЕу![]() дЫЖЏЖрЩйУыЪБЃЌЫФБпаЮ
дЫЖЏЖрЩйУыЪБЃЌЫФБпаЮ![]() ЪЧе§ЗНаЮ?жБНгаДГіНсТлЃЎ
ЪЧе§ЗНаЮ?жБНгаДГіНсТлЃЎ
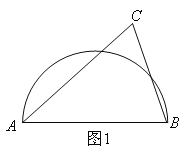
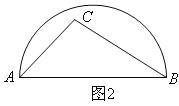
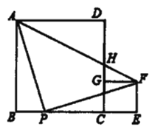
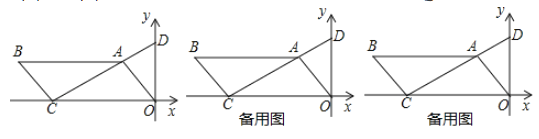
ЁОД№АИЁПЃЈ1ЃЉжБЯпACЕФНтЮіЪНЮЊ![]() ЃЛЃЈ2ЃЉЫФБпаЮPEFQЪЧОиаЮЃЌжЄУїМћНтЮіЃЛЃЈ3ЃЉЕуPдЫЖЏ
ЃЛЃЈ2ЃЉЫФБпаЮPEFQЪЧОиаЮЃЌжЄУїМћНтЮіЃЛЃЈ3ЃЉЕуPдЫЖЏ![]() УыЛђ
УыЛђ![]() УыЪБЃЌЫФБпаЮEPQFЪЧе§ЗНаЮ
УыЪБЃЌЫФБпаЮEPQFЪЧе§ЗНаЮ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓГіжБЯпACЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЯШРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯпOAЕФНтЮіЪНЃЌНјЖјЧѓГіЕуEЃЌFзјБъЃЌМДПЩЕУГіPE=FQЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉЯШЗжСНжжЧщПіЃЈЕуQдкЕуPзѓВрЛђгвВрЃЉЧѓГіPQЃЌРћгУPE=PQНЈСЂЗНГЬМДПЩЧѓГіЪБМфЃЎ
НтЃКЃЈ1ЃЉЩшжБЯпACЕФНтЮіЪНЮЊ![]()
ЁпЫФБпаЮABCOЪЧЦНааЫФБпаЮЃЌЧв![]() ЃЌ
ЃЌ![]()
ЁрOC=AB=9
ЁрCЃЈ-9ЃЌ0ЃЉ
Аб![]() ЁЂCЃЈ-9ЃЌ0ЃЉДњШы
ЁЂCЃЈ-9ЃЌ0ЃЉДњШы![]() ЕУЃК
ЕУЃК
Ёр![]()
Ёр![]()
ЁржБЯпACЕФНтЮіЪНЮЊ![]()
ЃЈ2ЃЉЃЉЫФБпаЮPEFQЪЧОиаЮЃЌРэгЩШчЯТЃК
ШчЭМ

ЁпЕуAЕФзјБъЮЊЃЈ-3ЃЌ3ЃЉ
ЁржБЯпOAЕФНтЮіЪНЮЊ![]()
ЁпЕуQДгЕуOГіЗЂвд1ИіЕЅЮЛ/УыбиxжсЯђзѓдЫЖЏ
ЁрOQ=-t
ЁрFЃЈ-tЃЌtЃЉ
ЁрFQ=t
ЁпЕуQДгЕуOГіЗЂвд1ИіЕЅЮЛ/УыбиxжсЯђзѓдЫЖЏЃЌ
ЁрOQ=-tЃЌ
ЁрFЃЈ-tЃЌtЃЉЃЌ
ЁрFQ=tЃЌ
ЁпЕуPДгЕуCГіЗЂвд2ИіЕЅЮЛ/УыбиxжсЯђгвдЫЖЏЃЌ
ЁрCP=2tЃЌ
ЁрOP=-9+2tЃЌ
гЩЃЈ1ЃЉжЊЃЌжБЯпACЕФНтЮіЪНЮЊ![]()
ЁрEЃЈ-9+2tЃЌtЃЉЃЌ
ЁрPE=tЃЌ
ЁрPE=FQЃЌ
ЁпFQЁЭxжсЃЌPEЁЭxжсЃЌ
ЁрЁЯPQF=90ЁуЃЌFQЁЮPEЃЌ
ЁпPE=FQЃЌ
ЁрЫФБпаЮPEFQЪЧЦНааЫФБпаЮЃЌ
ЁпЁЯPQF=90ЁуЃЌ
ЁрЦНааЫФБпаЮPEFQЪЧОиаЮ
ЁрЫФБпаЮPEFQЪЧОиаЮЃЛ
ЃЈ3ЃЉгЩЃЈ2ЃЉжЊЃЌPC=2tЃЌOQ=tЃЌPE=tЃЌ
ЁрPQ=OC-OQ-CP=9-t-2t=9-3tЃЌЛђPQ=OQ+CP-OC=3t-9ЃЌ
ЁпЫФБпаЮPEFQЪЧе§ЗНаЮЃЌ
ЁрPQ=PEЃЌ
Ёр9-3t=tЛђ3t-9=tЃЌ
Ёр![]() Лђ
Лђ![]() ЃЌМДЕуPдЫЖЏ
ЃЌМДЕуPдЫЖЏ![]() УыЛђ
УыЛђ![]() УыЪБЃЌЫФБпаЮEPQFЪЧе§ЗНаЮ
УыЪБЃЌЫФБпаЮEPQFЪЧе§ЗНаЮ

 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ