��Ŀ����
����Ŀ����������һ����������һ�������ڶԱ��ཻ�������뽻��֮����߶ΰ���������ηָ������С�����Σ�����ֵõ�����С��������һ��Ϊ���������Σ���һ����ԭ���������ƣ����ǰ������߶ν�����������ε������ߣ�
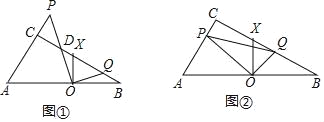
��1����ͼ���ڡ�ABC�У�ADΪ��ƽ���ߣ���B=50������C=30������֤��ADΪ��ABC����������
��2���ڡ�ABC�У���B=46����AD�ǡ�ABC�������ߣ��ҡ�ABD����ABΪ���ĵ��������Σ����BAC�Ķ�����
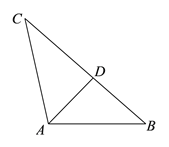
��3���ڡ�ABC�У�AB=4��AC=2��AD�ǡ�ABC�������ߣ��ҡ�ABD�ǵ��������Σ�ֱ��д��������AD�ij���
���𰸡�(1)��������(2) 113����(3) ![]() ��
��![]()
���������������:(1)���������ε������ߵĶ���,ֻҪ֤����ABD�ǵ���������,
��CAD����CBA���ɽ������,(2)��ͼ2��,���������������������AB=AD,
��CAD�ס�CBA,����B=��ADB=��CAD,��AC��BC,������ABC�������ì��, ����AB=BD, ��CAD�ס�CBA, (3)��ͼ3��,������������������AD=BD, ��CAD�ס�CBA,��![]() ��BD=AD=x,CD=y,�ɵ�
��BD=AD=x,CD=y,�ɵ�![]() ,�ⷽ�̼���, ����AB=AD=4,��
,�ⷽ�̼���, ����AB=AD=4,��![]() ,��BD=AD=x,CD=y,�ɵ�
,��BD=AD=x,CD=y,�ɵ�![]() ,�ⷽ�̼���, ����AB=AD,��Ȼ������.
,�ⷽ�̼���, ����AB=AD,��Ȼ������.
(1)֤����
�ߡ�B=50������C=30�������BAC=100����
��ADƽ�֡�BAC��
���BAD=��DAC=50����
���B=��BAD=50������DB=DA��
���ABD�ǵ��������Σ�
�ߡ�C=��C����DAC=��B=50����
���CAD�ס�CBA��
���߶�AD�ǡ�ABC�������ߣ�
��2����AB=AD����ȥ��
����������CAD�ס�CBA�����B=��ADB=��CAD����AC��BC����
��AB=BD����B=46����
���BAD=��BDA=67����
�ߡ�CAD�ס�CBA��
���CAD=��B=46����
���BAC=67��+46��=113����
��3��![]() ��
��![]() .
.

 �ƸԹھ��ο���ϵ�д�
�ƸԹھ��ο���ϵ�д�