Question

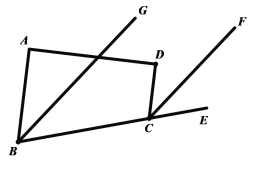
【题目】如图所示，在四边形中，的角平分线及外角的平分线所在的直线相交于点，若，．

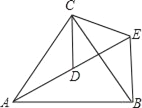
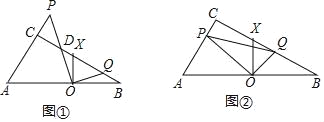
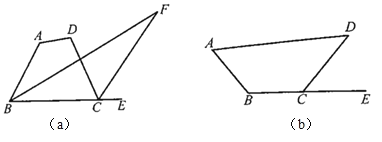
（1）如图(a)所示，，试用，表示，直接写出结论．

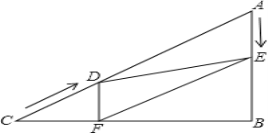
（2）如图(b)所示，，请在图中画出，并试用，表示．

（3）一定存在吗？若有，写出的值；若不一定，直接写出，满足什么条件时，不存在．

Answer 1

【答案】（1）；（2）图见解析，，证明见解析；（3）时，不存在，证明见解析．

【解析】

（1）先根据四边形的内角和求出，再根据角平分线的定义、邻补角的定义得出，然后根据三角形的外角性质即可得；

（2）先根据角平分线的定义画出图形，再参照题（1）：由四边形的内角和求出，再根据角平分线的定义、对顶角的性质得出，然后根据三角形的外角性质即可得；

（3）由题（1）和（2）可知，当和时，存在的值，因此，考虑当时，是否存在．证明如下：先根据四边形的内角和得出，再根据邻补角的定义得出，从而得出，然后根据角平分线的定义可得出，最后根据平行线的判定得出，即可得证．

（1），求解过程如下：

在四边形中，

平分，CF平分

；

（2）由题意，画的角平分线及外角的平分线所在的直线相交于点，则所要画的如下图所示．求解过程如下：

∵，且，

∴

∵平分，平分

∴

∵是的一个外角

∴

∴

；

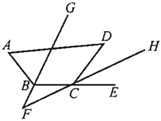
（3）当时，不存在．证明过程如下：

∵，且，

∴

∵平分，平分

∴

∴

故当时，不存在．