题目内容
【题目】如图1,在Rt△ABC中,∠ACB=90°,点D是边AB的中点,点E在边BC上,AE=BE,点M是AE的中点,联结CM,点G在线段CM上,作∠GDN=∠AEB交边BC于N.

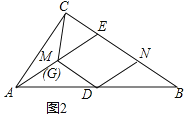
(1)如图2,当点G和点M重合时,求证:四边形DMEN是菱形;
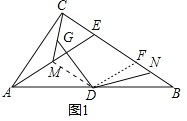
(2)如图1,当点G和点M、C不重合时,求证:DG=DN.
【答案】(1)见解析;(2)见解析
【解析】
本题主要考查菱形及全等三角形的应用
(1)先由MD为BE的中位线,可证MD∥EN且MD=![]() BE,又∠GDN+∠DNE=180°,可证四边形MDNE为平行四边形,从而可证平行四边形DMEN为菱形
BE,又∠GDN+∠DNE=180°,可证四边形MDNE为平行四边形,从而可证平行四边形DMEN为菱形
(2)取BE中点F,连接DM,DF,利用(1)的结论可证△DMG≌△DFN,即可得出答案
证明:(1)如图2中,
∵AM=ME.AD=DB,
∴DM∥BE,
∴∠GDN+∠DNE=180°,
∵∠GDN=∠AEB,
∴∠AEB+∠DNE=180°,
∴AE∥DN,
∴四边形DMEN是平行四边形,
∵![]() ,
,
∴DM=EM,
∴四边形DMEN是菱形.
(2)如图1中,取BE的中点F,连接DM、DF.
由(1)可知四边形EMDF是菱形,
∴∠AEB=∠MDF,DM=DF,
∴∠GDN=∠AEB,
∴∠MDF=∠GDN,
∴∠MDG=∠FDN,
∵∠DFN=∠AEB=∠MCE+∠CME,∠GMD=∠EMD+∠CME,、
在Rt△ACE中,∵AM=ME,
∴CM=ME,
∴∠MCE=∠CEM=∠EMD,
∴∠DMG=∠DFN,
∴△DMG≌△DFN,
∴DG=DN.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目