Question

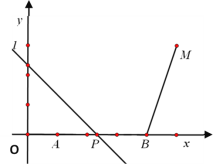
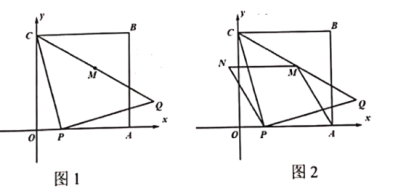
【题目】如图1，在平面直角坐标系中，正方形的边长为6，点分别在正半轴上，点在第一象限．点是正半轴上的一动点，且，连结，将线段绕点顺时针旋转90度至，连结，取中点．

（1）当时，求与的坐标．

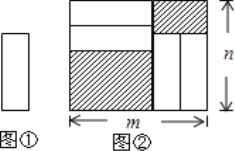
（2）如图2，连结，以、为邻边构造平行四边形记平行四边形的面积为．

①用含的代数式表示

②当落在的直角边上时，求的度数．

（3）在（2）的条件下，连结，记的面积为，若，则 (直接写出答案)

Answer 1

【答案】（1），；（2）①，②或；（3）或．

【解析】

（1）过点Q作轴于点D，首先证明，则有，进而可求出点F的坐标，再结合点C的坐标，即可求出M的坐标；

（2）①根据（1）中的全等三角形的性质得出M的坐标，然后利用即可求出答案；

②分两种情况：当N在PC上时和当N在PQ上时，分别利用全等三角形的性质和等腰直角三角形的性质求出∠CPM和∠MPA的度数，然后利用两角的和与差即可得出答案；

（3）过点M作轴于点H，过点Q作轴于点G，然后用含t的代数式表示出，然后分两种情况：点P在A点左侧和点P在A点右侧，分别建立关于t的一元二次方程求解即可．

（1）过点Q作轴于点D，

∵，

．

∵正方形边长为6，

，

．

由旋转的性质得， ，

，

．

，

．

在和中，

，

，

，

．

，

；

（2），

，

．

∵C（0,6），

∴M．

①当时，；

②当N在PC上时，

∵点M的横纵坐标相等，

∴点M在对角线OB上，

连结OM，

在和中，

∴CM=AM．

在Rt△CPQ中，M为CQ的中点，

∴PM⊥CQ，∠CPM=∠MPQ=45°，PM=CM=MQ，

∴PM=AM．

∵点N在PC上，NP∥AM，∠CPQ=90°，

∴AM⊥PQ，

∴∠PMA=45°，又PM=AM，

∴∠MPA=，

∴∠CPA=45°+67.5°=112.5°；

当N在PQ上时，同理可证MA=MP，∠AMP=45°，

∴∠MPA=，

∴∠CPA=67.5-45=22.5°，

综上所述，当点N在△CPQ的直角边上时，∠CPA的度数为112.5°或22.5°；

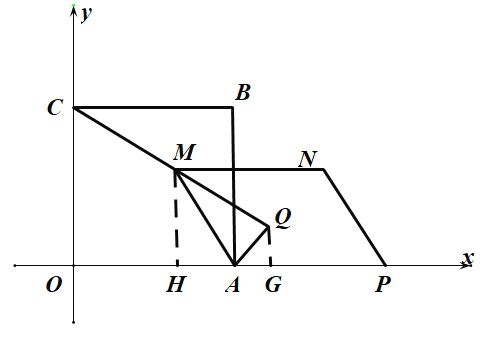
（3）过点M作轴于点H，过点Q作轴于点G，

当时，即点P在A点左侧时，如图

，

，

解得或（舍去）；

当时，即点P在A点右侧时，

，

，

，

解得或（舍去），

综上所述，t的值为或．