题目内容
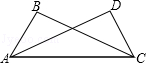
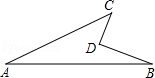
如图，已知△ABC≌△CDA，∠BAC=60°，∠DAC=23°，则∠D= ．
97°
试题分析：先由全等三角形的对应角相等得出∠BAC=∠DCA=60°，然后在△ADC中根据三角形内角和定理求出∠D的度数．
解：∵△ABC≌△CDA，
∴∠BAC=∠DCA=60°，∵∠DAC=23°
∴∠D=180°﹣∠DCA﹣∠DAC=97°．
故答案为97°．
点评：本题考查了全等三角形的性质及三角形内角和定理，根据全等三角形的对应角相等得出∠BAC=∠DCA=60°，是解题的关键．
练习册系列答案
天天练口算系列答案
相关题目
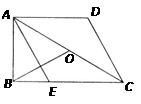
，AD=2，BC=3，下列结论：①∠CAE=30º；②AC=2AB；③S△ADC=2S△ABE；④BO⊥CD，其中正确的是（ ）