题目内容
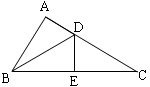
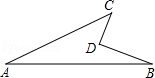
如图,这是一块农家菜地的平面图,其中BD=4m,CD=3m,AB=13m,AC=12m,∠BDC=90°,则这块地的面积为( )

| A.24m2 | B.30m2 | C.36m2 | D.42m2 |
A
试题分析:连接BC,在Rt△BDC中,已知BD,CD的长,运用勾股定理可求出BC的长,在△ABC中,已知三边长,运用勾股定理逆定理,可得此三角形为直角三角形,故四边形ABDC的面积为Rt△ACB与Rt△DBC的面积之差.
解:连接BC,
∵∠BDC=90°,BD=4m,CD=3m,
∴BC=5,
∵AB=13m,AC=12m,
∴AC2+BC2=122+52=169=132=AB2,
∴△ABC为直角三角形,
∴S四边形ABDC=S△ABC﹣S△BCD
=
 AC×BC﹣
AC×BC﹣ BD×CD
BD×CD=
 ×12×5﹣
×12×5﹣ ×4×3
×4×3=30﹣6
=24.
故选A.
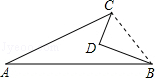
点评:本题考查的是勾股定理的逆定理及三角形的面积公式,根据题意作出辅助线,判断出△ACB的形状是解答此题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
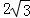 cm,则另一条直角边的长是( )
cm,则另一条直角边的长是( )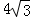 cm
cm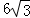 cm
cm